题目内容
14.已知函数f(x)=|x+2|+|x-3|(1)证明:f(x)≥f(0);
(2)若?x∈R,不等式3f(x)>f(a+1)恒成立,求实数a的取值范围.
分析 (1)分类讨论,求出f(x)的最小值,即可证明结论;
(2)?x∈R,不等式3f(x)≥f(a+1)恒成立,即?x∈R,不等式3[|x+2|+|x-3|]≥|a+3|+|a-2|恒成立,可得|a+3|+|a-2|≤15,分类讨论求实数a的取值范围.
解答 (1)证明:f(x)=|x+2|+|x-3|,
x≤-2时,f(x)=-x-2-x+3=-2x+1≥5,
-2<x<3时,f(x)=x+2-x+3=5,
x≥3时,f(x)=x+2+x-3=2x-1≥35,
∴f(x)≥5=f(0);
(2)解:?x∈R,不等式3f(x)≥f(a+1)恒成立,即?x∈R,不等式3[|x+2|+|x-3|]≥|a+3|+|a-2|恒成立,
∴|a+3|+|a-2|≤15,
a≤-3时,-a-3-a+2≤15,∴a≥-8,∴-8≤a≤-3,
-3<a<2时,a+3-a+2≤15,成立;
a≥2时,a+3+a-2≤15,∴a≤7,∴2≤a≤7,
综上所述,-8≤a≤7.
点评 本题考查了绝对值不等式的解法,考查恒成立问题、最值问题,是一道中档题.

练习册系列答案
相关题目
2.将A,B,C,D,E这5名同学从左至右排成一排,则A与B相邻且A与C之间恰好有一名同学的排法有( )
| A. | 18 | B. | 20 | C. | 21 | D. | 22 |
19.已知集合A={x|1<2x≤16},B={x|x<a},若A∩B=A,则实数a的取值范围是( )
| A. | a>4 | B. | a≥4 | C. | a≥0 | D. | a>0 |




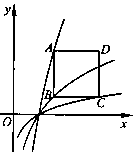 如图,已知正方形ABCD的边长为2,BC平行于x轴,顶点A,B和C分别在函数y1=3logax,y2=2logax和y3=logax(a>1)的图象上,则实数a的值为$\sqrt{2}$.
如图,已知正方形ABCD的边长为2,BC平行于x轴,顶点A,B和C分别在函数y1=3logax,y2=2logax和y3=logax(a>1)的图象上,则实数a的值为$\sqrt{2}$.