题目内容
已知直线l1:kx-y+
k=0与直线l2:x+k y-
=0的交点为P,(1)求点P的轨迹方程; (2)已知点Q(3,2),直线l:y=mx-2m+1 (m∈R)与点P的轨迹交于E、F两点,试判断
•
×tan∠EQF是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
| 5 |
| 5 |
| QE |
| QF |
考点:轨迹方程,平面向量数量积的运算
专题:综合题,直线与圆
分析:(1)直线l1:kx-y+
k=0过点A(-
,0),直线l2:x+k y-
=0过定点B(
,0),交点P的轨迹是以AB为直径的圆,可得点P的轨迹方程;
(2)
•
×tan∠EQF=|
||
|sin∠EQF=2S,故只要求S△EQF的最大值即可.
| 5 |
| 5 |
| 5 |
| 5 |
(2)
| QE |
| QF |
| QE |
| QF |
解答:
解:(1)由题意,直线l1:kx-y+
k=0过点A(-
,0),直线l2:x+k y-
=0过定点B(
,0),交点P的轨迹是以AB为直径的圆,∴求点P的轨迹方程为x2+y2=5; …(5分)
(2)
•
×tan∠EQF存在最大值.
•
×tan∠EQF=|
||
|sin∠EQF=2S,故只要求S△EQF的最大值即可 …(7分)
∵直线l:y=mx-2m+1 (m∈R)过定点(2,1),此点在点P的轨迹上,
不妨设为E,则可设直线l与圆的另一个交点为F(
cosθ,
sinθ),
由于
=(-1,-1),∴|
|=
…(9分)
又直线lQE:x-y-1=0,∴点F到直线lQE的距离d=
=
)-1|,
)≤
(当且仅当θ=2kπ-
,k∈Z时,取等号),…(11分)
∴S△EQF=
|
|d≤
,∴
•
×tan∠EQF最大值为
+1.…(12分)
| 5 |
| 5 |
| 5 |
| 5 |
(2)
| QE |
| QF |
| QE |
| QF |
| QE |
| QF |
∵直线l:y=mx-2m+1 (m∈R)过定点(2,1),此点在点P的轨迹上,
不妨设为E,则可设直线l与圆的另一个交点为F(
| 5 |
| 5 |
由于
| QE |
| QE |
| 2 |
又直线lQE:x-y-1=0,∴点F到直线lQE的距离d=
|
| ||||
|
=
|
| ||
| 4 |
| 2 |
| ||
|
| π |
| 4 |
∴S△EQF=
| 1 |
| 2 |
| QE |
| ||
| 2 |
| QE |
| QF |
| 10 |
点评:本题考查轨迹方程,考查圆的参数方程,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知数列1,
,
,2,
,…则3
是它的( )
| 2 |
| 3 |
| 5 |
| 3 |
| A、第25项 | B、第26项 |
| C、第27项 | D、第28项 |
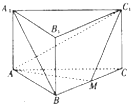 如图,已知三棱柱P-A1B1C1中,侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC的中点.
如图,已知三棱柱P-A1B1C1中,侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC的中点.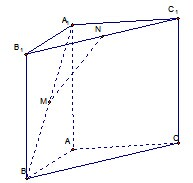 如图,直三棱柱ABC-A1B1C1,∠BAC=90°,AB=AC=
如图,直三棱柱ABC-A1B1C1,∠BAC=90°,AB=AC=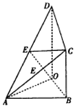 如图,△ABO是以AB为斜边的等腰直角三角形,OD⊥平面ABO,BC∥OD,且OD=2BC=2OA=2,E是AD中点,
如图,△ABO是以AB为斜边的等腰直角三角形,OD⊥平面ABO,BC∥OD,且OD=2BC=2OA=2,E是AD中点,