题目内容
已知:(2-x)6=a0+a1x+a2x2+…+a6x6.
(1)求a4;
(2)求a0+a1+a2+a3+a4+a5+a6的值;
(3)求|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|的值.
(1)求a4;
(2)求a0+a1+a2+a3+a4+a5+a6的值;
(3)求|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|的值.
考点:二项式系数的性质
专题:二项式定理
分析:(1)根据二项式(2-x)6 展开式的通项公式,求得a4的值.
(2)令x=1,可得a0+a1+a2+a3+a4+a5+a6 的值.
(3)令x=-1得:|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=36=729,而a0=64,从而求得|a1|+|a2|+|a3|+|a4|+|a5|+|a6|的值.
(2)令x=1,可得a0+a1+a2+a3+a4+a5+a6 的值.
(3)令x=-1得:|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=36=729,而a0=64,从而求得|a1|+|a2|+|a3|+|a4|+|a5|+|a6|的值.
解答:
解:(1)由于二项式(2-x)6 展开式的通项公式为 Tr+1=
•26-r•(-1)r•xr,
所以,a4=
•22=60.
(2)令x=1,得a0+a1+a2+a3+a4+a5+a6 =1.
(3)令x=-1得:|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=36=729,
而 a0=64,
所以,|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=665.
| C | r 6 |
所以,a4=
| C | 4 6 |
(2)令x=1,得a0+a1+a2+a3+a4+a5+a6 =1.
(3)令x=-1得:|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=36=729,
而 a0=64,
所以,|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=665.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知曲线y=2x3上一点A(1,2),则A处切线的斜率是( )
| A、2 | B、3 | C、4 | D、6 |
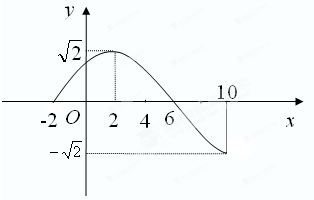 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<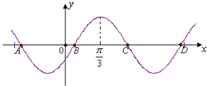 已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,点B(
已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,点B(