题目内容

在△ABC中，若sinB：sinC=3：4，则边c：b=
 
．
考点：正弦定理
专题：解三角形
分析：利用正弦定理把角的正弦转化为三角形的边，即可．
解答： 解：由正弦定理知
b
sinB
=
c
sinC
=2R，
∴b=2RsinB，c=sinC•2R，
∴c：b=sinC：sinB=4：3，
故答案为：4：3
点评：本题主要考查了正弦定理的应用．正弦定理和余弦定理在解三角形问题中常用来完成边角问题的转化．
练习册系列答案
相关题目
画出函数y=2 
1
x
的图象．
若△ABC三内角A，B，C所对的三边长分别为a，b，c，且面积S△ABC=
1
4
（b2+c2-a2），求角A．
已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，8b=5c，∠C=2∠B，求cosC．
已知向量
a
，
b
满足|
a
|=3，|
b
|=2
3
，且
a
⊥（
a
+
b
），则
b
在
a
方向上的投影
 
．
a，b，c表示直线，M表示平面，给出下列四个命题：
①若a∥M，b∥M，则a∥b；   
②若b?M，a∥b，则a∥M；
③若a⊥c，b⊥c，则a∥b；     
④若a⊥M，b⊥M，则a∥b．
其中正确命题的序号是
 
（请将你认为正确的结论的序号都填上）．
若函数f（x）=logm（msin2x-2msinx+3）（x∈R）的值总不是负数，则实数m的取值范围是
 
．
函数f（x）的定义域是[-1，1]，则函数F（x）=f（1-x）的定义域是
 
．
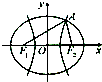如图，F1，F2是双曲线C1：x2-
y2
3
=1与椭圆C2的公共焦点，点A是C1，C2在第一象限的公共点．若|F1F2|=|F1A|，则C2的离心率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网