题目内容
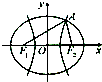 如图,F1,F2是双曲线C1:x2-
如图,F1,F2是双曲线C1:x2-| y2 |
| 3 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用双曲线与椭圆的定义及其离心率计算公式即可得出.
解答:
解:由双曲线C1:x2-
=1可得a1=1,b1=
,c=2.
设椭圆C2的方程为
+
=1,(a>b>0).
则|F1A|-|F2A|=2a1=2,|F1A|+|F2A|=2a,
∴2|F1A|=2a+2
∵|F1F2|=|F1A|=2c=4,
∴2×4=2a+2,解得a=3.
则C2的离心率=
=
.
故答案为:
.
| y2 |
| 3 |
| 3 |
设椭圆C2的方程为
| x2 |
| a2 |
| y2 |
| b2 |
则|F1A|-|F2A|=2a1=2,|F1A|+|F2A|=2a,
∴2|F1A|=2a+2
∵|F1F2|=|F1A|=2c=4,
∴2×4=2a+2,解得a=3.
则C2的离心率=
| c |
| a |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查了双曲线与椭圆的定义及其离心率计算公式,属于基础题.

练习册系列答案
相关题目
 重庆某中学高二年级共有学生800名,现在从该校高二年级学生中随机抽取100名学生,将他们数学学业水平考试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.据此统计,该校高二年级学生数学学业水平考试成绩不低于及格分数(60分)的学生人数为( )
重庆某中学高二年级共有学生800名,现在从该校高二年级学生中随机抽取100名学生,将他们数学学业水平考试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.据此统计,该校高二年级学生数学学业水平考试成绩不低于及格分数(60分)的学生人数为( )