题目内容
8.以圆C1:x2+y2+4x+1=0与圆C2:x2+y2+2x+2y+1=0相交的公共弦为直径的圆的方程为( )| A. | (x-1)2+(y-1)2=1 | B. | (x+1)2+(y+1)2=1 | C. | (x+$\frac{3}{5}$)2+(y+$\frac{6}{5}$)2=$\frac{4}{5}$ | D. | (x-$\frac{3}{5}$)2+(y-$\frac{6}{5}$)2=$\frac{4}{5}$ |
分析 两圆方程相减求出公共弦所在直线的解析式,确定公共弦为直径的圆的圆心坐标,即可得出结论.
解答 解:圆C1:x2+y2+4x+1=0与圆C2:x2+y2+2x+2y+1=0,方程相减得圆C1与圆C2的公共弦所在直线的方程:x-y=0.
与圆C1:x2+y2+4x+1=0联立,可得圆2x2+4x+1=0,∴x1+x1=-2,∴公共弦为直径的圆的圆心坐标为(-1,-1),
故选:B,
点评 此题考查了直线与圆相交的性质,求出公共弦所在的直线方程是解本题的关键.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
16.若向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-1,2),则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为( )
| A. | (1,5) | B. | (1,1) | C. | (3,1) | D. | (3,5) |
17.已知圆O:x2+y2+6x-2y+6=0,若斜率存在且不等于0的直线l过点A(4,0)且被圆O截得的弦长为2$\sqrt{3}$,则直线l的方程为( )
| A. | 24x+7y-28=0 | B. | 7x+24y-28=0 | C. | 24x-7y-28=0 | D. | 7x-24y-28=0 |
18.若${log_a}\frac{4}{5}<1$(a>0,且a≠1),则实数a的取值范围是( )
| A. | $(0,\frac{4}{5})$ | B. | $(\frac{4}{5},+∞)$ | C. | $(\frac{4}{5},1)$ | D. | $(0,\frac{4}{5})∪(1,+∞)$ |
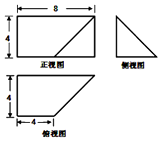 一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.
一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.