题目内容
5.已知椭圆E的中心为坐标原点,离心率为$\frac{1}{2}$,E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|=( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
分析 利用椭圆的离心率以及抛物线的焦点坐标,求出椭圆的半长轴,然后求解抛物线的准线方程,求出A,B坐标,即可求解所求结果.
解答 解:椭圆E的中心在坐标原点,离心率为$\frac{1}{2}$,E的右焦点(c,0)与抛物线C:y2=8x的焦点(2,0)重合,
可得c=2,a=4,b2=12,椭圆的标准方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$,
抛物线的准线方程为:x=-2,
代入椭圆方程,解得y=±3,所以A(-2,3),B(-2,-3).
∴|AB|=6.
故选:B.
点评 本题考查抛物线以及椭圆的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
13.已知函数f(x)=(x2-4)(x-a),a为实数,f′(1)=0,则f(x)在[-2,2]上的最大值是( )
| A. | $\frac{9}{2}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | $\frac{50}{27}$ |
10.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x},x≥0}\\{lo{g}_{3}(-x),x<0}\end{array}\right.$,函数g(x)=f2(x)+f(x)+t(t∈R).关于函数g(x)的零点,下列判断不正确的是( )
| A. | 若t<-2,g(x)有四个零点 | B. | 若t=-2,g(x)有三个零点 | ||
| C. | 若-2<t<$\frac{1}{4}$,g(x)有两个零点 | D. | 若t=$\frac{1}{4}$,g(x)有一个零点 |
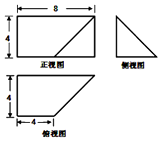 一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.
一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.