若a=20.5.b=log0.25.c=0.52.则a.b.c三个数的大小关系式( )A．c＜a＜bB．b＜c＜aC．c＜b＜aD．b＜a＜c 题目和参考答案——青夏教育精英家教网——

题目内容

8．若a=2^0.5，b=log_0.25，c=0.5²，则a、b、c三个数的大小关系式（　　）

A．

c＜a＜b

B．

b＜c＜a

C．

c＜b＜a

D．

b＜a＜c

分析利用指数函数与对数函数的单调性即可得出．

解答解：∵a=2^0.5＞1，b=log_0.25＜0，c=0.5²∈（0，1），
则a＞c＞b．
故选：B．

点评本题考查了指数函数与对数函数的单调性，考查了推理能力与计算能力，属于基础题．

练习册系列答案

天天练习王口算题卡心算速算巧算系列答案

通城学典初中课外文言文阅读系列答案

名师学案英语阅读系列答案

口算题卡加应用题一日一练系列答案

53题霸专题集训系列答案

中考现代文阅读系列答案

语文全真模拟试卷系列答案

小学数学知识集锦系列答案

实战演练卷系列答案

口算小状元口算速算天天练系列答案

相关题目

18．若i是虚数单位，则计算$\frac{1+7i}{2-i}$的结果为（　　）

19．椭圆$\frac{{x}^{2}}{4}$+y²=1的离心率为（　　）

$\frac{\sqrt{3}}{2}$

$\frac{\sqrt{5}}{2}$

16．若向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为（　　）

3．已知x＞-2，则x+$\frac{1}{x+2}$的最小值为（　　）

13．已知函数f（x）=（x²-4）（x-a），a为实数，f′（1）=0，则f（x）在[-2，2]上的最大值是（　　）

$\frac{50}{27}$

20．函数f（x）=$\frac{\sqrt{2-x}}{{log}_{2}x}$的定义域为（　　）

{x|0＜x≤2且x≠1}

{x|0＜x＜2且x≠1}

17．已知圆O：x²+y²+6x-2y+6=0，若斜率存在且不等于0的直线l过点A（4，0）且被圆O截得的弦长为2$\sqrt{3}$，则直线l的方程为（　　）

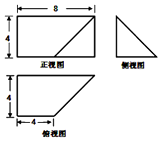一个几何体的三视图如图所示（单位：cm），则该几何体的表面积为64+32$\sqrt{2}$cm²，体积为$\frac{160}{3}$cm．