在△ABC中.若a2=b2+c2-$\sqrt{3}$bc.则角A的度数为( )A．30°B．150°C．60°D．120° 题目和参考答案——青夏教育精英家教网—

题目内容

14．在△ABC中，若a²=b²+c²-$\sqrt{3}$bc，则角A的度数为（　　）

A．

30°

B．

150°

C．

60°

D．

120°

分析利用余弦定理即可得出．

解答解：∵a²=b²+c²-$\sqrt{3}$bc，
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\sqrt{3}bc}{2bc}$=$\frac{\sqrt{3}}{2}$，A∈（0°，180°）．
∴A=30°，
故选：A．

点评本题考查了余弦定理的应用，考查了推理能力与计算能力，属于中档题．

练习册系列答案

相关题目

4．“点P（1，2）在曲线x²+a²y²-5=0上”是“a=1”的（　　）

	A．	充分非必要条件		B．	必要非充分条件
	C．	充要条件		D．	既非充分又非必要条件

5．纸张的规格是指纸张制成后，经过修整切边，裁成一定的尺寸．现在我国采用国际标准，规定以A₀，A₁，A₂，B₁，B₂，…等标记来表示纸张的幅面规格．复印纸幅面规格只采用A系列和B系列，其中An（n∈N，n≤8）系列的幅面规格为：
①A₀，A₁，A₂，…，A₈所有规格的纸张的幅宽（以x表示）和长度（以y表示）的比例关系都为$x：y=1：\sqrt{2}$；
②将A₀纸张沿长度方向对开成两等分，便成为A₁规格，A₁纸张沿长度方向对开成两等分，便成为A₂规格，…，如此对开至A₈规格．现有A₀，A₁，A₂，…，A₈纸各一张．若A₄纸的宽度为2dm，则A₀纸的面积为64$\sqrt{2}$dm²；这9张纸的面积之和等于$\frac{511\sqrt{2}}{4}$dm²．

2．在△ABC中，内角A、B、C所对的边长分别是a、b、c，且边c的长为2，角C为$\frac{π}{3}$，△ABC的面积为$\sqrt{3}$，则a=（　　）

9．设复数z=$\frac{1}{1-i}$+i（i为虚数单位），则|z|=（　　）

$\frac{\sqrt{10}}{2}$

D．

19．设不等式x²-x≤0的解集为M，则M为（　　）

6．已知函数f（x）=（x-1）e^x．
（1）求f（x）的单调区间；
（2）求f（x）在区间[0，1]上的最大值与最小值．

3．

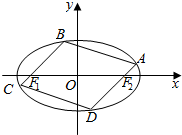已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），两点F₁（-1，0）、F₂（1，0）为椭圆C的焦点，点P在椭圆C上，且|PF₁|+|PF₂|=2|F₁F₂|．
（1）求椭圆C的标准方程；
（2）如图已知椭圆C的内接平行四边形ABCD的一组对边分别过椭圆的焦点F₁、F₂，求该平行四边形ABCD面积的最大值．

4．复数z=$\frac{a-i}{1+i}$（a∈R，i是虚数单位）在复平面上对应的点不可能位于（　　）

试题分类