题目内容
根据下列关系,求各个数列{an}的通项公式:
(1)a1=4,an+1=
an;
(2)a1=2,an-1-an=2anan-1.
(1)a1=4,an+1=
| n+1 |
| n+3 |
(2)a1=2,an-1-an=2anan-1.
考点:数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:(1)由an+1=
an,可得
=
,利用叠乘法,可求数列的通项;
(2)取倒数,可得{
}是以
为首项,2为公差的等差数列,可求数列{an}的通项.
| n+1 |
| n+3 |
| an+1 |
| an |
| n+1 |
| n+3 |
(2)取倒数,可得{
| 1 |
| an |
| 1 |
| 2 |
解答:
解:(1)∵an+1=
an,
∴
=
,
∴an=a1•
•…•
=4•
•
•…•
=
;
(2)∵an-1-an=2anan-1,
∴
-
=2,
∵a1=2,
∴{
}是以
为首项,2为公差的等差数列,
∴
=
+2(n-1)=
,
∴an=
.
| n+1 |
| n+3 |
∴
| an+1 |
| an |
| n+1 |
| n+3 |
∴an=a1•
| a2 |
| a1 |
| an |
| an-1 |
| 2 |
| 4 |
| 3 |
| 5 |
| n |
| n+2 |
| 24 |
| (n+1)(n+2) |
(2)∵an-1-an=2anan-1,
∴
| 1 |
| an |
| 1 |
| an-1 |
∵a1=2,
∴{
| 1 |
| an |
| 1 |
| 2 |
∴
| 1 |
| an |
| 1 |
| 2 |
| 4n-3 |
| 2 |
∴an=
| 2 |
| 4n-3 |
点评:本题考查数列递推式,考查等差数列的判断,考查叠乘法,正确选用求数列通项的方法是关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
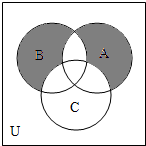 如图所示,已知集合A、B、C为全集U的子集,则图中阴影部分所表示的集合为( )
如图所示,已知集合A、B、C为全集U的子集,则图中阴影部分所表示的集合为( )| A、(∁∪C)∪(A∪B) |
| B、(A∪B)∩[∁∪(A∩B)] |
| C、(A∪B)∩[∁∪(A∩B∩C)] |
| D、{A∩[∁∪(B∪C)]}∪{B∩[∁∪(A∪C)]} |
若两个集合A、B是非空集合,则“A∩B=B”是“A∪B=A”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知x,y满足约束条件
,那么z=2x+3y的最小值为( )
|
A、
| ||
| B、8 | ||
C、
| ||
| D、10 |