题目内容
3.已知正六边形ABCDEF的边长为1,则$\overrightarrow{AB}•\overrightarrow{AC}$的值为( )| A. | $-\frac{3}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{2}$ |
分析 可先画出图形,并连接AC,这样在△ABC中,根据AB=BC=1,∠BAC=30°即可求出AC的长度,从而便可求出$\overrightarrow{AB}•\overrightarrow{AC}$的值.
解答 解:如图,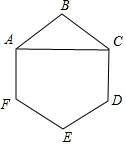
在△ABC中,AB=BC=1,∠BAC=30°;
∴$AC=2cos30°=\sqrt{3}$;
∴$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cos30°$=$1×\sqrt{3}×\frac{\sqrt{3}}{2}=\frac{3}{2}$.
故选D.
点评 考查三角函数的定义,清楚正六边形的内角为120°,以及向量数量积的计算公式.

练习册系列答案
相关题目
13.公比为2的正项等比数列{an},a3a11=16,则a5=( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
14.在△ABC中,已知a=$\sqrt{2}$,c=2,A=30°,则C等于( )
| A. | 45° | B. | 45°或135° | C. | 30° | D. | 30°或150° |
11.已知圆${x^2}+{y^2}+(4-2a)x-2\sqrt{3}ay+4{a^2}-4a-12=0$,定直线l经过点A(1,0),若对任意的实数a,定直线l被圆C截得的弦长始终为定值d,求得此定值d等于( )
| A. | $2\sqrt{7}$ | B. | $\sqrt{31}$ | C. | $\sqrt{34}$ | D. | $\sqrt{37}$ |
8.如图所示,程序据图(算法流程图)的输出结果为( )
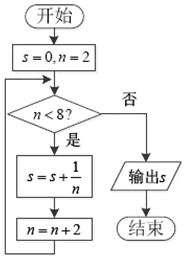

| A. | $\frac{3}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{11}{12}$ | D. | $\frac{25}{24}$ |
13.设全集A={1,2,3,4,5},B={2,4,6,8,10},则A∪B=( )
| A. | {2,4} | B. | {1,2,3,4,5,6,8,10} | ||
| C. | {1,2,3,4,5} | D. | {2,4,6,8,10} |
 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.