题目内容
18. 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.(1)设AD=x(x>0),求用x表示AE的函数关系式;
(2)设AD=x(x>0),ED=y,求用x表示y的函数关系式;
(3)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请说明理由.
分析 (1)根据DE把草坪分成面积相等的两部分,利用任意三角形的面积公式建立关系即可.
(2)利用余弦定理建立关系即可.
解答 解:(1)由题意:DE把草坪分成面积相等的两部分,AD=x,
∴${S_{△ADE}}=\frac{1}{2}{S_{△ABC}}$,即$\frac{1}{2}x•AE•sin{60°}=\frac{{\sqrt{3}}}{2}$,∴$AE=\frac{2}{x}$(x>0),…①
(2)AD=x(x>0),ED=y,在△ADE中,y2=x2+AE2-2x•AE•cos60°,即y2=x2+AE2-x•AE,②
①代入②得:${y^2}={x^2}+{(\frac{2}{x})^2}-2$(y>0),∴$y=\sqrt{{x^2}+{{(\frac{2}{x})}^2}-2}$(1≤x≤2).
(3)如果DE是水管,$y=\sqrt{{x^2}+{{(\frac{2}{x})}^2}-2}≥\sqrt{2×2-2}=\sqrt{2}$,
当且仅当${x^2}=\frac{4}{x^2}$,即$x=\sqrt{2}$时“=”成立,故${y_{min}}=\sqrt{2}$,
即DE∥BC,且$AD=DE=\sqrt{2}$时,DE最短;
如果DE是参观线路,记$f(x)={x^2}+\frac{4}{x^2}$,
根据勾勾函数的图象及性质,可知函数在$[1,\sqrt{2}]$上递减,在$[\sqrt{2},2]$上递增,
故f(x)max=f(1)=f(2)=5,
∴${y_{max}}=\sqrt{5-2}=\sqrt{3}$,
即DE为AB中线或AC中线时,DE最长.
点评 本题考查余弦定理和基本不等式的性质以及函数的思想在实际问题中的运用和关系的建立.属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $-\frac{3}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{2}$ |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
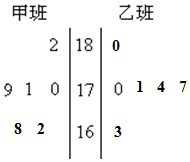 随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.