题目内容
 已知an=(
已知an=(| 1 |
| 3 |
考点:归纳推理,等比数列的通项公式
专题:创新题型
分析:本题是数列题,已知数列的通项公式,根据条件给出的几何图形中的规律,求出某个数在数列中的项数,从而求出该项.
解答:
解:将三角形状中各个数从上到下,从左到右依次展开,排成一列,得到a1,a2,a3,a4…
设第m行的第n个数A(m,n)是数列{an}中的第k项,
由于第一行有1个数,第二行有3个数,第三行有5个数,…,第(m-1)行有(2m-3)个数.
其中1,3,5,…(2m-3),成等差数列,首项为1,公差为2.
则:k=1+3+5+…+(2m-3)+n=
×(m-1)+n=(m-1)2+n.
A(10,12)中,m=10,n=12,
k=1+3+5+…+17+12=
×9+12=92+12=93
由通项公式an=(
)n得:
A(10,12)=(
)93.
故答案为:(
)93.
设第m行的第n个数A(m,n)是数列{an}中的第k项,
由于第一行有1个数,第二行有3个数,第三行有5个数,…,第(m-1)行有(2m-3)个数.
其中1,3,5,…(2m-3),成等差数列,首项为1,公差为2.
则:k=1+3+5+…+(2m-3)+n=
| 1+(2m-3) |
| 2 |
A(10,12)中,m=10,n=12,
k=1+3+5+…+17+12=
| 1+17 |
| 2 |
由通项公式an=(
| 1 |
| 3 |
A(10,12)=(
| 1 |
| 3 |
故答案为:(
| 1 |
| 3 |
点评:本题考查了归纳推理和数列通项公式的应用,重点是用数列的通项公式求数列的某一项,难点是项数的研究,要善于发现项数的规律.

练习册系列答案
相关题目
已知一元二次不等式f(x)≤0的解集为{x|x≤
,或x≥3},则f(ex)>0的解集为( )
| 1 |
| 2 |
| A、{x|x<-ln2,或x>ln3} |
| B、{x|ln2<x<ln3} |
| C、{x|x<ln3}} |
| D、{x|-ln2<x<ln3} |
各项均为正数的数列{an}的前n项和Sn,且3Sn=anan+1,则
a2k=( )
| n |
 |
| i=1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
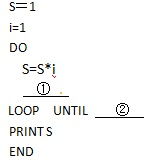

 有一个奇数组成的数阵排列如图:则第30行从左到右第3个数是
有一个奇数组成的数阵排列如图:则第30行从左到右第3个数是