题目内容
已知数列{an}的前n项和为Sn,且满足
=
(a是常数且a>O,a≠2),bn=
+1.
(1)求数列{an}的通项公式;
(2)若数列{bn}为等比数列,求{bn}的通项公式;
(3)在(2)的条件下,记cn=log3b1+log3b2+…+log3bn,?n∈N*是否存在正整数m,使
+
+…+
≥
都成立?若存在,求出m的值;若不存在,请说明理由.
| Sn |
| an-2 |
| a |
| a-2 |
| 2Sn |
| an |
(1)求数列{an}的通项公式;
(2)若数列{bn}为等比数列,求{bn}的通项公式;
(3)在(2)的条件下,记cn=log3b1+log3b2+…+log3bn,?n∈N*是否存在正整数m,使
| 1 |
| c1 |
| 1 |
| c2 |
| 1 |
| cn |
| m |
| 3 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(1)利用a1=S1,当n≥2时,an=Sn-Sn-1及其等比数列的定义即可得出;
(2)利用bn=
+1及其an可得b1,b2,b3.由于数列{bn}为等比数列,可得
=b1b3.即可得出a.再利用等比数列的通项公式即可得出.
(3)利用对数的运算法则、等差数列的前n项和公式、“裂项求和”即可得出.
(2)利用bn=
| 2Sn |
| an |
| b | 2 2 |
(3)利用对数的运算法则、等差数列的前n项和公式、“裂项求和”即可得出.
解答:
解:(1)由得:Sn=
(an-2)
∴a1=
(a1-2),
解得a1=a.
当n≥2时,∴an=Sn-Sn-1=
(an-2)-
(an-1-2),
化为
=
,
∴数列{an}是首项为a,公比为
的等比数列.
∴an=a•(
)n-1.
(2)∵bn=
+1,
∴b1=
+1=3,
b2=
+1=2+a+1=3+a,
b3=
+1=2+a+2×(
)2+1=
+a+3,
∵数列{bn}为等比数列,∴
=b1b3.
∴(3+a)2=3(
+a+3),
化为a2-6a=0,又a>0.
解得a=6.
∴公比q=
=
=3.
∴bn=3n.
(3)证:cn=log3b1+log3b2+…+log3bn=log3b1b2…bn=log331+2+…+n=
,
∴
+
+…+
=2[(1-
)+(
-
)+…+(
-
)]=2(1-
),
由
+
+…+
≥
?n∈N*都成立得:
2(1-
)≥
,对?n∈N*都成立,
∵数列{
}是单调递减数列,
∴2(1-
)≥
,即1≥
.
∵m是正整数,∴m的值为1、2、3.
| a |
| a-2 |
∴a1=
| a |
| a-2 |
解得a1=a.
当n≥2时,∴an=Sn-Sn-1=
| a |
| a-2 |
| a |
| a-2 |
化为
| an |
| an-1 |
| a |
| 2 |
∴数列{an}是首项为a,公比为
| a |
| 2 |
∴an=a•(
| a |
| 2 |
(2)∵bn=
| 2Sn |
| an |
∴b1=
| 2a1 |
| a1 |
b2=
| 2(a1+a2) |
| a1 |
b3=
| 2(a1+a2+a3) |
| a1 |
| a |
| 2 |
| a2 |
| 2 |
∵数列{bn}为等比数列,∴
| b | 2 2 |
∴(3+a)2=3(
| a2 |
| 2 |
化为a2-6a=0,又a>0.
解得a=6.
∴公比q=
| b2 |
| b1 |
| 3+6 |
| 3 |
∴bn=3n.
(3)证:cn=log3b1+log3b2+…+log3bn=log3b1b2…bn=log331+2+…+n=
| n(n+1) |
| 2 |
∴
| 1 |
| c1 |
| 1 |
| c2 |
| 1 |
| cn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
由
| 1 |
| c1 |
| 1 |
| c2 |
| 1 |
| cn |
| m |
| 3 |
2(1-
| 1 |
| n+1 |
| m |
| 3 |
∵数列{
| 1 |
| n+1 |
∴2(1-
| 1 |
| 2 |
| m |
| 3 |
| m |
| 3 |
∵m是正整数,∴m的值为1、2、3.
点评:本题考查了利用“当n≥2时,an=Sn-Sn-1”求递推关系、等差数列与等比数列的定义通项公式及其前n项和公式、“裂项求和”、对数的运算法则等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
已知一元二次不等式f(x)≤0的解集为{x|x≤
,或x≥3},则f(ex)>0的解集为( )
| 1 |
| 2 |
| A、{x|x<-ln2,或x>ln3} |
| B、{x|ln2<x<ln3} |
| C、{x|x<ln3}} |
| D、{x|-ln2<x<ln3} |
 如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,点E、F、G分别是各自所在棱的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,点E、F、G分别是各自所在棱的中点.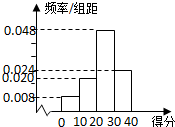 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如下: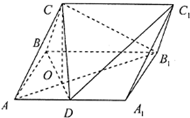 在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=