题目内容
11. 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直.AB=$\sqrt{2}$,AF=1.M是线段EF的中点
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直.AB=$\sqrt{2}$,AF=1.M是线段EF的中点(1)求证:BD⊥AM
(II)求证:AM∥平面BDE;
(III)求三棱锥A-BDF的体积.
分析 (1)根据面面垂直的性质证明BD⊥平面ACEF,根据线面垂直的性质得出BD⊥AM.
(2)取AC,BD交点O,连结OE,则四边形AOEM是平行四边形,得到AM∥OE,推出AM∥平面BDE.
(3)以△ABD为棱锥底面,则棱锥的高为FA,代入体积公式计算.
解答 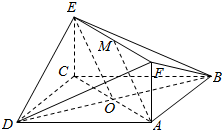 证明:(I)∵四边形ABCD是正方形,∴BD⊥AC,
证明:(I)∵四边形ABCD是正方形,∴BD⊥AC,
又∵平面ABCD⊥平面ACEF,平面ABCD∩平面ACEF=AC,
∴BD⊥平面ACFE,∵AM?平面ACEF,
∴BD⊥AM.
(II)设AC,BD交于点O,连结EO.
∵四边形ABCD是正方形,∴AO=$\frac{1}{2}AC$,
∵M是EF中点,∴ME=$\frac{1}{2}$EF,
∵四边形ACEF是矩形,∴AC=EF,AC∥EF.
∴AO∥ME,AO=ME,
∴四边形AOEM是平行四边形,
∴AM∥OE,∵OE?平面BDE,AM?平面BDE,
∴AM∥平面BDE.
(III)V棱锥A-BDF=V棱锥F-ABD=$\frac{1}{3}{S}_{△ABD}•FA$=$\frac{1}{3}×\frac{1}{2}×{(\sqrt{2})}^{2}×1$=$\frac{1}{3}$.
点评 本题考出查了线面平行,线面垂直的判定,面面垂直的性质,几何体的体积计算,属于中档题.

练习册系列答案
相关题目
16.在三棱锥P-ABC中,底面△ABC为正三角形,且PA=PB=PC,G为△PAC的重心,过G作三棱锥的一个截面,使截面平行于直线AC与PB,若截面是边长为2的正方形,则三棱锥的体积为( )
| A. | $\frac{3\sqrt{3}}{3}$ | B. | $\frac{9\sqrt{11}}{4}$ | C. | $\frac{16\sqrt{2}}{3}$ | D. | 18$\sqrt{2}$ |
1.下面四个条件中,使a>b成立的充分不必要条件是( )
| A. | |a|>|b| | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | a2>b2 | D. | lga>lgb |