题目内容
已知点A（-3，-2）和圆C：（x-4）2+（y-8）2=9，一束光线从点A发出，射到直线l：y=x-1后反射（入射点为B），反射光线经过圆周C上一点P，则折线ABP的最短长度是 ．
考点：圆的标准方程
专题：直线与圆
分析：求出A点关于直线l：y=x-1的对称点D，连接D与圆C的圆心，交圆C于P，则折线ABP的最短长度等于|DC|-3．
解答：
解：如图：
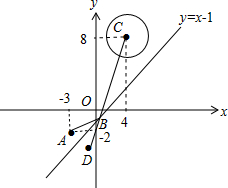
设A（-3，-2）关于直线l：y=x-1的对称点为D（x0，y0），
由
，解得D（-1，-4），
由圆的方程可知圆心为C（4，8），半径为3．
连接DC交圆C于P，
则|DC|=
=13．
∴折线ABP的最短长度是13-3=10．
故答案为：10．
设A（-3，-2）关于直线l：y=x-1的对称点为D（x0，y0），
由
|
由圆的方程可知圆心为C（4，8），半径为3．
连接DC交圆C于P，
则|DC|=
| (4+1)2+(8+4)2 |
∴折线ABP的最短长度是13-3=10．
故答案为：10．
点评：本题考查了圆的标准方程，考查了直线和圆的位置关系，考查了数形结合的解题思想方法与数学转化思想方法，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=sin（
-2x），x∈R是（ ）
| π |
| 2 |
| A、最小正周期为π的奇函数 | ||
B、最小正周期为
| ||
| C、最小正周期为π的偶函数 | ||
D、最小正周期为
|
袋中装有4个大小相同、标号分别为1，2，3，4的小球，依次从袋中取出所有的球，则“标号顺序不符合从小到大或从大到小排列”的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|