题目内容
若双曲线
-
=1上一点P到左焦点距离是8,则点P到y轴的距离是 .
| x2 |
| 64 |
| y2 |
| 36 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据双曲线的标准方程得,a=8,b=6,c=10,设左右焦点分别为F1,F2,则|8-|PF2||=16,所以|PF2|=24,设P(x,y),则
,解出x即得点P到y轴的距离.
|
解答:
解:根据双曲线方程得:a=8,b=6,c=10,∴设左焦点F1(-10,0),右焦点F2(10,0);
∴根据双曲线的定义:||PF1|-|PF2||=16,P到右焦点的距离是24,设P(x,y),则:
,解得x=-
;
∴点P到y轴的距离是
.
故答案为:
.
∴根据双曲线的定义:||PF1|-|PF2||=16,P到右焦点的距离是24,设P(x,y),则:
|
| 64 |
| 5 |
∴点P到y轴的距离是
| 64 |
| 5 |
故答案为:
| 64 |
| 5 |
点评:考查双曲线的标准方程,三个参数a,b,c的关系:a2+b2=c2,以及双曲线的定义:||PF1|-|PF2||=2a,及两点之间距离公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,a、b、c分别是∠A、∠B、∠C的对边,若C=60°,3a=2c=6,则b值为( )
A、
| ||
B、
| ||
C、
| ||
D、1+
|
若实数x,y满足约束条件
,则函数z=|x+y+1|的最小值是( )
|
| A、0 | ||
| B、4 | ||
C、
| ||
D、
|
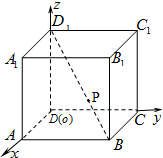 如图在棱长为1正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系Oxyz,
如图在棱长为1正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系Oxyz, 如图,DC⊥平面ABC,∠BAC=90°,AC=
如图,DC⊥平面ABC,∠BAC=90°,AC=