题目内容
由直线y=x+2上的点向圆（x-2）2+（y+2）2=1引切线，则切线长的最小值为（ ）
A、
| ||
| B、4 | ||
C、3
| ||
D、
|
考点：圆的切线方程
专题：直线与圆
分析：由题意画出图形，在直角三角形CMP中，由斜边最短则直角边最短可得，当P为过圆心作直线y=x+2的垂线的垂足时切线最短，然后由点到直线的距离公式求出PC，再利用勾股定理得答案．
解答：
解：如图，
过直线y=x+2上的点P向圆（x-2）2+（y+2）2=1引切线PM，
连接CM，要使切线PM最小，
则直线y=x+2上的点P与圆心C的距离最小，
圆心C（2，-2）到直线y=x+2的距离d=
=3
．
∴切线长的最小值为
=
．
故选：A．
解：如图，过直线y=x+2上的点P向圆（x-2）2+（y+2）2=1引切线PM，
连接CM，要使切线PM最小，
则直线y=x+2上的点P与圆心C的距离最小，
圆心C（2，-2）到直线y=x+2的距离d=
| |2+2+2| | ||
|
| 2 |
∴切线长的最小值为
(3
|
| 17 |
故选：A．
点评：本题考查了圆的切线方程，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
已知f（x）是R上的奇函数，当x∈[0，+∞）时，f（x）=x+sinx，当x∈（-∞，0]，f（x）解析式为（ ）
| A、-x-sinx |
| B、x+sinx |
| C、-x+sinx |
| D、x-xsin |
已知函数f（x）=
，若f′（1）=0，则a等于（ ）
| x2+a |
| x+1 |
| A、3 | B、-3 | C、2 | D、-2 |
已知a=20.3，b=log0.50.24，c=0.32，则a，b，c的大小关系正确的是（ ）
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜a＜b |
| D、b＜c＜a |
若三点A（2，3），B（3，4），C（a，b）共线，则有（ ）
| A、a=3，b=-5 |
| B、a-b+1=0 |
| C、2a-b=3 |
| D、a-2b=0 |
函数y=
的定义域为（ ）
| ||
| tanx |
| A、（0，3] | ||||
| B、（0，π） | ||||
C、（0，
| ||||
D、[0，
|
已知f（x）=
，则f（-8）等于（ ）
|
| A、-1 | B、0 | C、1 | D、2 |
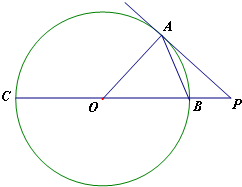如图，点A在直径为15的⊙O上，PBC是过点O的割线，且PA=10，PB=5．
如图，AB是圆O的直径，点C在圆O上，延长BC到D使BC=CD，过C作圆O的切线交AD于E．若AB=10，ED=3，求BC的长．