题目内容
已知f(x)=ax2-3x-4
(1)f(x)≥0在a∈[1,2]上恒成立,求x的范围.
(2)f(x)≥0在x∈[1,2]上恒成立,求a的范围.
(3)解关于x的不等式:f(x)≥0.
(1)f(x)≥0在a∈[1,2]上恒成立,求x的范围.
(2)f(x)≥0在x∈[1,2]上恒成立,求a的范围.
(3)解关于x的不等式:f(x)≥0.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)解不等式即可,(2)中将a≥
转化为求函数y=
的最值问题,(3)里的解不等式问题需将a分情况进行讨论.
| 3x+4 |
| x2 |
| 3x+4 |
| x2 |
解答:
解:(1)f(x)≥0在a∈[1,2]上恒成立
令g(a)=ax2-3x-4,
∴
,
即
,
解得:x≥4,或x≤-1.
∴x的范围为:{x|x≥4,或x≤-1}.
(2)f(x)≥0在x∈[1,2]上恒成立
?ax2-3x-4≥0在x∈[1,2]上恒成立
a≥
在x∈[1,2]上恒成立
y=
=4×(
)2+3(
),
∈[
,1]
ymax=7,
故a的范围是[7,∞).
(3)由ax2-3x-4≥0
①a>0时,△=9+16a>0恒成立,
解集为:{x|x≥
或x≤
},
②a=0时,解集为:{x|x≤-
},
③-
≤a<0时,
解集为:{x|
≤x≤
},
④a<-
时,
解集为:∅.
令g(a)=ax2-3x-4,
∴
|
即
|
解得:x≥4,或x≤-1.
∴x的范围为:{x|x≥4,或x≤-1}.
(2)f(x)≥0在x∈[1,2]上恒成立
?ax2-3x-4≥0在x∈[1,2]上恒成立
a≥
| 3x+4 |
| x2 |
y=
| 3x+4 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
ymax=7,
故a的范围是[7,∞).
(3)由ax2-3x-4≥0
①a>0时,△=9+16a>0恒成立,
解集为:{x|x≥
3+
| ||
| 2a |
3-
| ||
| 2a |
②a=0时,解集为:{x|x≤-
| 4 |
| 3 |
③-
| 9 |
| 16 |
解集为:{x|
3+
| ||
| 2a |
3-
| ||
| 2a |
④a<-
| 9 |
| 16 |
解集为:∅.
点评:本题考察了二次函数的性质问题,解题过程中用到了转化思想,分类讨论思想.

练习册系列答案
相关题目
已知a=20.3,b=log0.50.24,c=0.32,则a,b,c的大小关系正确的是( )
| A、a<b<c |
| B、b<a<c |
| C、c<a<b |
| D、b<c<a |
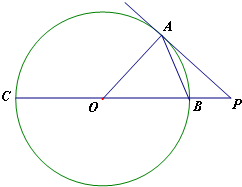 如图,点A在直径为15的⊙O上,PBC是过点O的割线,且PA=10,PB=5.
如图,点A在直径为15的⊙O上,PBC是过点O的割线,且PA=10,PB=5. 如图,已知AB⊥平面ACD,DE⊥平面ACD,AB=2,AC=AD=DE=4,F为CD的中点,
如图,已知AB⊥平面ACD,DE⊥平面ACD,AB=2,AC=AD=DE=4,F为CD的中点, 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=10,ED=3,求BC的长.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=10,ED=3,求BC的长.