题目内容
14.定义一个对应法则f:P(m,n)→P'($\sqrt{m}$,$\sqrt{n$)(m≥0,n≥0),比如P(2,4)→P'($\sqrt{2}$,2),已知点A(2,6)和点B(6,2),M是线段AB上的动点,点M在法则f下的对应点为M',当M在线段AB上运动时,点M'的轨迹为( )| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 抛物线的一部分 |
分析 根据所给的两个点的坐标写出直线的方程,设出两个点的坐标,根据所给的对应法则得到两个点坐标之间的关系,代入直线的方程得到轨迹方程.
解答 解:由题意知点A(6,2)和点B(2,6),AB的方程为:y-6=-(x-2),即x+y-8=0
设M′(x,y),则M(x2,y2),当M在线段AB上运动时,
从而有y2+x2-8=0,x∈[2,6],y∈[2,6],轨迹方程是圆的一部分.
故选:B.
点评 本题以定义的一种新的变换为入手点,主要考查直线与圆的有关知识,解答本题的关键是弄懂定义的本质.

练习册系列答案
相关题目
2.已知复数z满足(1+i)•z=2-i(其中i为虚数单位),则|z|=( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{10}$ |
9.sin40°sin10°+cos40°sin80°=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | cos50° | D. | $\frac{{\sqrt{3}}}{2}$ |
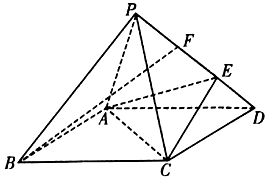 19、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.
19、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.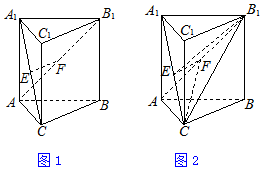 如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.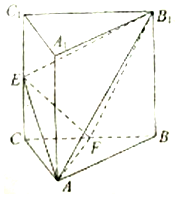 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.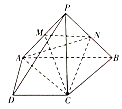 如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥
如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥