题目内容

2．已知复数z满足（1+i）•z=2-i（其中i为虚数单位），则|z|=（　　）
A．$\frac{{\sqrt{5}}}{2}$B．$\frac{{\sqrt{10}}}{2}$C．$\frac{{3\sqrt{2}}}{2}$D．$\sqrt{10}$

分析 利用复数的运算法则、共轭复数的定义、模的计算公式即可得出．

解答 解：（1+i）•z=2-i，∴（1-i）（1+i）•z=（1-i）（2-i），∴2z=3-3i，解得z=$\frac{3}{2}$-$\frac{3}{2}$i．
则|z|=$\sqrt{（\frac{3}{2}）^{2}×2}$=$\frac{3\sqrt{2}}{2}$．
故选：C．

点评 本题考查了复数的运算法则、共轭复数的定义、模的计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
12．已知函数f（x）=ax-lnx，F（x）=ex+ax，其中x＞0，a＜0，e为自然对数的底数．
（Ⅰ）若f（x）和F（x）在区间（0，ln3）内具有相同的单调性，求实数a的取值范围；
（Ⅱ）若$a∈（{-∞，-\frac{1}{e^2}}]$，且函数g（x）=xeax-1-2ax+f（x）的最小值为M，求M的最小值．
13．已知向量$\overrightarrow a=（1，2）$，$\overrightarrow b=（-2，1）$，则（　　）
A．$\overrightarrow a∥\overrightarrow b$B．$\overrightarrow a⊥\overrightarrow b$C．$\overrightarrow a$与$\overrightarrow b$的夹角为60°D．$\overrightarrow a$与$\overrightarrow b$的夹角为30°
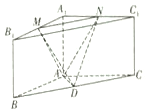10．在△ABC中，CB=5，AD⊥BC交BC于点D，若CD=2时，则$\overrightarrow{CA}•\overrightarrow{CB}$=（　　）
A．5B．2C．10D．15
17．如下图所示的三棱柱ABC-A1B1C1中，棱AA1⊥底面A1B1C1，AB=AC=AA1，∠ABC=30°，M，N，D分别是A1B1，A1C1，BC的中点．
（Ⅰ）求证：MN⊥AD；
（Ⅱ）求为二面角M-AD-N的余弦值．
7．已知正项等比数列{an}的公比q＞1，且满足a2=6，a1a3+2a2a4+a3a5=900，设数列{an}的前n项和为Sn，若不等式λan≤1+Sn对一切n∈N*恒成立，则实数λ的最大值为$\frac{4}{3}$．
14．定义一个对应法则f：P（m，n）→P'（$\sqrt{m}$，$\sqrt{n$）（m≥0，n≥0），比如P（2，4）→P'（$\sqrt{2}$，2），已知点A（2，6）和点B（6，2），M是线段AB上的动点，点M在法则f下的对应点为M'，当M在线段AB上运动时，点M'的轨迹为（　　）
A．线段B．圆的一部分C．椭圆的一部分D．抛物线的一部分
11．设函数y=f（x）图象上不同两点A（x1，y1），B（x2，y2）处的切线的斜率分别是kA，kB，规定φ（A，B）=$\frac{{|{k_A}-{k_B}|}}{|AB|}$（|AB|为线段AB的长度）叫做曲线y=f（x）在点A与点B之间的“弯曲度”，给出以下命题：
①函数y=x3图象上两点A与B的横坐标分别为1和-1，则φ（A，B）=0；
②存在这样的函数，图象上任意两点之间的“弯曲度”为常数；
③设点A，B是抛物线y=x2+1上不同的两点，则φ（A，B）≤2；
④设曲线y=ex（e是自然对数的底数）上不同两点A（x1，y1），B（x2，y2），则φ（A，B）＜1．
其中真命题的序号为①②③④．（将所有真命题的序号都填上）
12．已知函数f（x）=x3+ax2+bx（x＞0）的图象与x轴相切于点（3，0）．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若g（x）+f（x）=-6x2+（3c+9）x，命题p：?x1，x2∈[-1，1]，|g（x1）-g（x2）|＞1为假命题，求实数c的取值范围；
（Ⅲ）若h（x）+f（x）=x3-7x2+9x+clnx（c是与x无关的负数），判断函数h（x）有几个不同的零点，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网