题目内容
18.在△ABC中,∠C=90°,BC=2,M为BC的中点,sin∠BAM=$\frac{1}{3}$,则AC的长为$\sqrt{2}$.分析 作出图象,设出未知量,在△ABM中,由正弦定理可得sin∠AMB=$\frac{c}{3}$,进而可得cosβ=sin∠AMB,在RT△ACM中,还可得cosβ=$\frac{b}{\sqrt{1+{b}^{2}}}$,再由勾股定理可得c=$\sqrt{4+{b}^{2}}$,继而解得b的值
解答 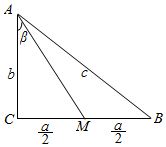 解:如图
解:如图
设AC=b,AB=c,CM=MB=$\frac{a}{2}$=1,∠MAC=β,
在△ABM中,由正弦定理可得$\frac{BM}{sin∠BAM}$=$\frac{c}{sin∠AMB}$=$\frac{1}{\frac{1}{3}}$=3
解得sin∠AMB=$\frac{c}{3}$,
故cosβ=cos($\frac{π}{2}$-∠AMC)=sin∠AMC=sin(π-∠AMB)=sin∠AMB=$\frac{c}{3}$,
而在RT△ACM中,cosβ=$\frac{AC}{AM}$=$\frac{b}{\sqrt{1+{b}^{2}}}$,
故可得$\frac{b}{\sqrt{1+{b}^{2}}}$=$\frac{c}{3}$,
再由勾股定理可得a2+b2=c2,即c=$\sqrt{4+{b}^{2}}$,
故9b2=(1+b2)(4+b2),
解得b=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查正弦定理的应用,涉及三角函数的诱导公式以及勾股定理的应用,属中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.已知椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点分别为F1,F2,M为C上位于第一象限的点,|MF1|=2,且MF1⊥y轴,MF2与椭圆C交于另一点N,若$\overrightarrow{M{F}_{2}}$=2$\overrightarrow{{F}_{2}N}$,则直线MN的斜率为( )
| A. | -$\frac{\sqrt{5}}{2}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
4.cos80°cos130°-cos10°sin130°等于( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
2.若${y^3}{(x+\frac{1}{xy})^n}(n∈{N^*})$的展开式中存在常数项,则常数项为( )
| A. | 15 | B. | 20 | C. | 30 | D. | 120 |
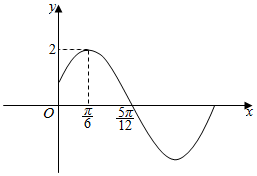 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.