题目内容

4．cos80°cos130°-cos10°sin130°等于（　　）
A．-$\frac{1}{2}$B．$\frac{1}{2}$C．-$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{3}}{2}$

分析 利用诱导公式，两角差的余弦函数公式化简，利用特殊角的三角函数值即可计算求值．

解答 解：cos80°cos130°-cos10°sin130°
=cos80°cos130°-sin80°sin130°
=cos（80°+130°）
=cos（180°+30°）
=-$\frac{\sqrt{3}}{2}$．
故选：C．

点评 本题主要考查了诱导公式，两角差的余弦函数公式，特殊角的三角函数值在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．

练习册系列答案
相关题目
20．如图，在圆x2+y2=1上任取一点P，过点P作x轴的垂线段DM，D为垂足，点P为线段DM的中点．
（1）当点P在圆x2+y2=1上运动时，求点M的轨迹C的方程；
（2）在（1）的条件下，证明：点M的轨迹C的所有外切矩形的顶点在一个定圆上．
1．已知函数f（x）=sinx（-$\frac{π}{2}$$＜x＜\frac{π}{2}$），满足f（x）＜$\frac{\sqrt{3}}{2}$的x的取值范围是（　　）
A．（-$\frac{π}{6}$，$\frac{π}{6}$）B．（-$\frac{π}{2}$，$\frac{π}{6}$）C．（-$\frac{π}{2}$，$\frac{π}{3}$）D．（-$\frac{π}{3}$，$\frac{π}{3}$）
18．在△ABC中，∠C=90°，BC=2，M为BC的中点，sin∠BAM=$\frac{1}{3}$，则AC的长为$\sqrt{2}$．
5．若一组数据2，4，6，8的中位数、方差分别为m，n，且ma+nb=1（a＞0，b＞0），则$\frac{1}{a}$+$\frac{1}{b}$的最小值为（　　）
A．6+2$\sqrt{3}$B．4$+3\sqrt{5}$C．9$+4\sqrt{5}$D．20
9．数列{an}的前n项和为Sn，若对任意n∈N*，都有${S_n}={（-1）^n}{a_n}+\frac{1}{2^n}+n-3$，则数列{a2n-1}的前n项和为$\frac{1}{{2}^{n-2}}$-$\frac{1}{{4}^{n}}$-3+2n．
16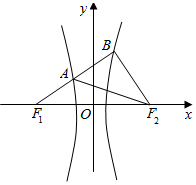．已知F1，F2分别为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点，若存在过F1的直线分别交双曲线C的左、右支于A，B两点，使得∠BAF2=∠BF2F1，则双曲线C的离心率e的取值范围是（　　）
A．（3，+∞）B．（1，2+$\sqrt{5}$）C．（3，2+$\sqrt{5}$）D．（1，3）
13．若复数z满足z=$\frac{|8+6i|}{6-8i}$（i是虚数单位），则z的虚部为（　　）
A．4B．$\frac{4}{5}$C．-4D．-$\frac{4}{5}$
14．若实数x，y满足不等式组$\left\{\begin{array}{l}x+3y-3≤0\\ x-y+1≥0\\ y≥1\end{array}\right.$，则z=2|x|+y的取值范围是（　　）
A．[-1，3]B．[1，3]C．[-1，11]D．[-5，11]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网