题目内容
1.已知函数$f(x)=\frac{{\sqrt{3}}}{2}sin2x-{cos^2}x-\frac{1}{2}$.(Ⅰ)求f(x)的最小正周期和单调增区间;
(Ⅱ)当x∈[-$\frac{π}{12}$,$\frac{5π}{12}$]时,求函数f(x)的最小值和最大值.
分析 (Ⅰ)由三角函数公式化简可得f(x)=sin(2x-$\frac{π}{6}$)-1,由周期公式可得周期,解2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$可得单调增区间;
(Ⅱ)由x∈[-$\frac{π}{12}$,$\frac{5π}{12}$]可得2x-$\frac{π}{6}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],可得sin(2x-$\frac{π}{6}$)∈[-$\frac{\sqrt{3}}{2}$,1],可得答案.
解答 解:(Ⅰ)化简可得$f(x)=\frac{{\sqrt{3}}}{2}sin2x-{cos^2}x-\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$(1+cos2x)-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x-1
=sin(2x-$\frac{π}{6}$)-1,
∴f(x)的最小正周期T=$\frac{2π}{2}$=π,
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$可得kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$
∴函数的单调增区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$]k∈Z;
(Ⅱ)当x∈[-$\frac{π}{12}$,$\frac{5π}{12}$]时,2x-$\frac{π}{6}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
∴sin(2x-$\frac{π}{6}$)∈[-$\frac{\sqrt{3}}{2}$,1],
∴函数f(x)的最小值和最大值分别为-$\frac{\sqrt{3}}{2}$-1和0.
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和最值,属中档题.

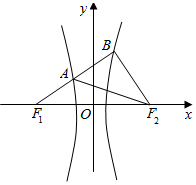 已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )
已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )| A. | (3,+∞) | B. | (1,2+$\sqrt{5}$) | C. | (3,2+$\sqrt{5}$) | D. | (1,3) |
| A. | 14 | B. | 18 | C. | 12 | D. | 16 |
| A. | 4 | B. | $\frac{4}{5}$ | C. | -4 | D. | -$\frac{4}{5}$ |
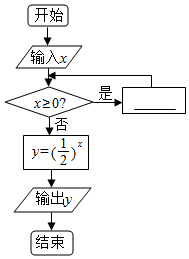 已知①x=x-1,②x=x-2,③x=x-3,④x=x-4在如图所示的程序框图中,如果输入x=10,而输出y=4,则在空白处可填入( )
已知①x=x-1,②x=x-2,③x=x-3,④x=x-4在如图所示的程序框图中,如果输入x=10,而输出y=4,则在空白处可填入( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ②③④ |