题目内容
19.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{6}}}{2}$,则它的渐近线方程为( )| A. | y=±2x | B. | y=±$\frac{1}{4}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{{\sqrt{2}}}{2}$x |
分析 由双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{6}}}{2}$,可得c=$\frac{{\sqrt{6}}}{2}$a,求出b,即可求出双曲线的渐近线方程.
解答 解:∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{6}}}{2}$,
∴$\frac{c}{a}$=$\frac{{\sqrt{6}}}{2}$,∴c=$\frac{{\sqrt{6}}}{2}$a,
∴b=$\sqrt{\frac{3}{2}{a}^{2}-{a}^{2}}$=$\frac{\sqrt{2}}{2}$a,
∴双曲线的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x.
故选D.
点评 本题主要考查双曲线的简单性质的应用,属于基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
7.已知函数f(x)=3x2-2ax-8在(1,2)上不单调,则实数a的取值范围是( )
| A. | [3,6] | B. | (-∞,3]∪[6,+∞) | C. | [3,6) | D. | (3,6) |
11.若正三棱柱的所有棱长均为4,则其体积为( )
| A. | $\frac{{16\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $8\sqrt{3}$ | D. | $16\sqrt{3}$ |
 试写出函数f(x)=x${\;}^{\frac{1}{2}}$的性质,并作出它的大致图象.
试写出函数f(x)=x${\;}^{\frac{1}{2}}$的性质,并作出它的大致图象.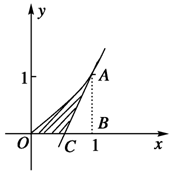 在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围成的面积为$\frac{1}{12}$,试求:
在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围成的面积为$\frac{1}{12}$,试求: