题目内容
在区间[-2π，2π]范围内，函数y=tanx与函数y=sinx的图象交点的个数为（ ）
| A、3 | B、5 | C、7 | D、9 |
考点：正弦函数的图象,正切函数的图象
专题：函数的性质及应用
分析：直接由tanx=sinx，解方程即可得到结论．
解答：
解：tanx=sinx得
=sinx，
即sinx（
-1）=0，
即sinx=0或
=1，
∴sinx=0或cosx=1．
∴在区间[-2π，2π]内x=-2π，-π，0，π，2π共5个值．
故两个函数图象的交点个数为5个．
故选：B．
| sinx |
| cosx |
即sinx（
| 1 |
| cosx |
即sinx=0或
| 1 |
| cosx |
∴sinx=0或cosx=1．
∴在区间[-2π，2π]内x=-2π，-π，0，π，2π共5个值．
故两个函数图象的交点个数为5个．
故选：B．
点评：本题主要考查函数图象交点个数的判断，利用函数和方程之间的关系，直接解方程即可．
练习册系列答案
相关题目
下列函数中，在区间（0，2）上是增函数的是（ ）
| A、y=x2-4x+5 | ||
B、y=
| ||
| C、y=2-x | ||
D、y=log
|
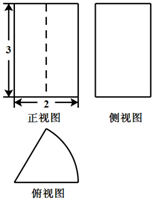某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的体积为（ ）A、
| ||
B、
| ||
| C、π | ||
| D、2π |
已知双曲线
-
=1的左焦点为F1，点P为双曲线右支上一点，且PF1与圆x2+y2=16相切于点N，M为线段PF1的中点，O为坐标原点，则|MN|-|MO|的值为（ ）
| x2 |
| 16 |
| y2 |
| 25 |
| A、2 | B、-1 | C、1 | D、-2 |
在等比数列{an}中，a7•a12=5，则a8•a9•a10•a11=（ ）
| A、10 | B、25 | C、50 | D、75 |
抛物线y2=
x上的一点M到焦点的距离为1，则点M到y轴的距离是（ ）
| 1 |
| 4 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
下列曲线的离心率是
的是（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
S与T是两个非空集合，且S?T，令Z=S∩T，则S∪Z为（ ）
| A、Z | B、T | C、∅ | D、S |
佛山某中学高三（1）班排球队和篮球队各有10名同学，现测得排球队10人的身高（单位：cm）分别是：162、170、171、182、163、158、179、168、183、168，篮球队10人的身高（单位：cm）分别是：170、159、162、173、181、165、176、168、178、179．