题目内容
已知向量
=(cos
,-1),
=(
sin
,cos2
),设函数f(x)=
•
+
(1)若x∈[0,
],f(x)=
,求cosx的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2bcosA≤2c-
a,求f(B)的取值范围.
| m |
| x |
| 2 |
| n |
| 3 |
| x |
| 2 |
| x |
| 2 |
| m |
| n |
| 1 |
| 2 |
(1)若x∈[0,
| π |
| 2 |
| ||
| 3 |
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2bcosA≤2c-
| 3 |
考点:两角和与差的余弦函数,平面向量数量积的运算
专题:三角函数的求值
分析:(1)利用平面向量的数量积的坐标运算可求得f(x)=sin(x-
),依题意易求cos(x-
)=
,借助两角和的余弦公式即可求得cosx的值;
(2)由2bcosA≤2c-
a得:cosB≥
,从而可得B的取值范围,利用正弦函数的单调性质即可求得f(B)的取值范围.
| π |
| 6 |
| π |
| 6 |
| ||
| 3 |
(2)由2bcosA≤2c-
| 3 |
| ||
| 2 |
解答:
解:(1)依题意得f(x)=sin(x-
),
由x∈[0,
]得:-
≤x-
≤
,sin(x-
)=
>0,
从而可得cos(x-
)=
,
则cosx=cos[(x-
)+
]=cos
cos(x-
)-sin
sin(x-
)=
-
;
(2)由2bcosA≤2c-
a得:2b•
≤2c-
a,即c2+a2-b2=2accosB≥
ac,
∴cosB≥
,从而0<B≤
,
故f(B)=sin(B-
)∈(-
,0].
| π |
| 6 |
由x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| ||
| 3 |
从而可得cos(x-
| π |
| 6 |
| ||
| 3 |
则cosx=cos[(x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| ||
| 6 |
(2)由2bcosA≤2c-
| 3 |
| b2+c2-a2 |
| 2bc |
| 3 |
| 3 |
∴cosB≥
| ||
| 2 |
| π |
| 6 |
故f(B)=sin(B-
| π |
| 6 |
| 1 |
| 2 |
点评:本题考查平面向量的数量积的坐标运算,考查两角和的余弦及正弦函数的单调性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知复数z满足条件:(1+2i)z=1,则z对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
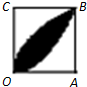 在正方形OABC框格内有一块花纹(如图所示),花纹刚好过点O,B,经研究发现花纹边界是函数y=x2与
在正方形OABC框格内有一块花纹(如图所示),花纹刚好过点O,B,经研究发现花纹边界是函数y=x2与 四边形ABCD是圆O的内接四边形,点O在BD上,已知∠ABC=60°,AD=
四边形ABCD是圆O的内接四边形,点O在BD上,已知∠ABC=60°,AD= 某市政府为了了解居民的生活用电情况,以使全市在用电高峰月份的居民生活不受影响,决定制定一个合理的月均用电标准.为了确定一个较为合理的标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,其样本统计结果如下图表:
某市政府为了了解居民的生活用电情况,以使全市在用电高峰月份的居民生活不受影响,决定制定一个合理的月均用电标准.为了确定一个较为合理的标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,其样本统计结果如下图表: