题目内容
已知圆C的方程为(x-2)2+(y-1)2=25,A(3,4)为定点,过A的两条弦MN、PQ互相垂直,记四边形MPNQ面积的最大值与最小值分别为S1,S2,则
-
是( )
| S | 2 1 |
| S | 2 2 |
| A、200 | B、100 |
| C、64 | D、36 |
考点:直线与圆的位置关系
专题:计算题,数形结合,直线与圆
分析:画出图形,先确定MN2+PQ2为定值,表示出面积,即可求四边形ABCD的面积的最大值和最小值.
解答:
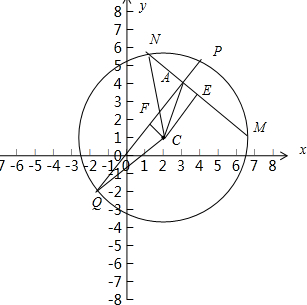 解:圆C的方程为(x-2)2+(y-1)2=25,
解:圆C的方程为(x-2)2+(y-1)2=25,
圆心坐标C(2,1),半径R=5
设弦MN,PQ的中点分别为E,F,
则CE2+CF2=CA2=(3-2)2+(4-1)2=10,
CE2+NE2=CF2+QF2=25,
NE2+QF2=(25-CE2)+(25-CF2)=50-(CE2+CF2)=40,
MN2+PQ2=4(NE2+QF2)=160
∴S2=
MN2×PQ2=
MN2×(160-MN2),
MN2∈[60,100].
当MN2=80时,S2取得最大值:S12=1600.
当MN2=60时,S2取得最小值:S22=1500.
则
-
=1600-1500=100
故选:B.
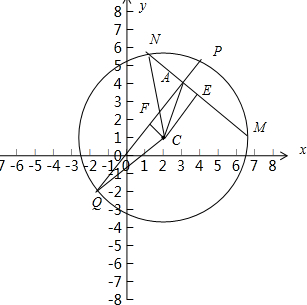 解:圆C的方程为(x-2)2+(y-1)2=25,
解:圆C的方程为(x-2)2+(y-1)2=25,圆心坐标C(2,1),半径R=5
设弦MN,PQ的中点分别为E,F,
则CE2+CF2=CA2=(3-2)2+(4-1)2=10,
CE2+NE2=CF2+QF2=25,
NE2+QF2=(25-CE2)+(25-CF2)=50-(CE2+CF2)=40,
MN2+PQ2=4(NE2+QF2)=160
∴S2=
| 1 |
| 4 |
| 1 |
| 4 |
MN2∈[60,100].
当MN2=80时,S2取得最大值:S12=1600.
当MN2=60时,S2取得最小值:S22=1500.
则
| S | 2 1 |
| S | 2 2 |
故选:B.
点评:本题考查直线与圆的位置关系,考查面积的计算,最值的应用,考查数形结合以及转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
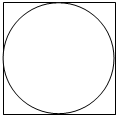 如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )
如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )A、1-
| ||
| B、π | ||
C、
| ||
D、1-
|
直线l与直线l1:x-3y+10=0和直线l2:2x+y-8=0分别交于M,N两点,且MN的中点坐标为(0,1),则直线l的方程为( )
| A、x+4y-4=0 |
| B、4x+y-4=0 |
| C、x-4y+4=0 |
| D、x-4y-4=0 |
到点A(1,1,1)、B(-1,-1,-1)的距离相等的点C(x,y,z)的坐标满足( )
| A、x+y+z=-1 |
| B、x+y+z=0 |
| C、x+y+z=1 |
| D、x+y+z=3 |