题目内容
在平面直角坐标系xOy中,直线l:ax+by+c=0被圆C:x2+y2=16截得的弦的中点为M,若a+3b-c=0.则OM2的最大值是 .
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:(1)根据直线和圆相交的性质,利用条件消去参数a,b,c,得到点M的轨迹方程,即可得出结论.
解答:
解:若直线l:ax+by+c=0被圆C:x2+y2=16截得的弦的中点为M,则满足OM⊥l,
设M(x,y),则
=
,即a=
,
∵a+3b-c=0,
∴c=a+3b=
+3b,
将a,c代入直线ax+by+c=0得
x+by+
+3b=0,
整理得x2+y2+x+3y=0,
故点M的轨迹方程为x2+y2+x+3y=0,即(x+0.5)2+(y+1.5)2=2.5
∴OM2的最大值为2.5.
故答案为:2.5
设M(x,y),则
| y |
| x |
| b |
| a |
| bx |
| y |
∵a+3b-c=0,
∴c=a+3b=
| bx |
| y |
将a,c代入直线ax+by+c=0得
| bx |
| y |
| bx |
| y |
整理得x2+y2+x+3y=0,
故点M的轨迹方程为x2+y2+x+3y=0,即(x+0.5)2+(y+1.5)2=2.5
∴OM2的最大值为2.5.
故答案为:2.5
点评:本题主要考查与圆有关的轨迹问题.利用直线和圆的位置关系是解决本题的关键.

练习册系列答案
相关题目
执行如图所示的程序框图,若输入的x的值为-
,则输出的i的值为( )
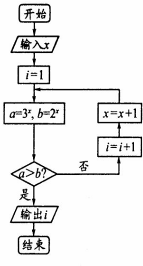
| 3 |
| 2 |

| A、4 | B、3 | C、2 | D、1 |
已知不等式
表示的平面区域的面积为2,则
的最小值为( )
|
| x+y+2 |
| x+1 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
若非空集合A中的元素具有命题α的性质,集合B中的元素具有命题β的性质,若A?B,则命题α是命题β的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、不充分不必要条件 |
 如图是某正五棱台灯罩的俯视图,在A,B,C,D,E五个侧面上装裱3种不同的透明中国山水画,相邻区域的中国山水画不同,则不同的装裱方案数是
如图是某正五棱台灯罩的俯视图,在A,B,C,D,E五个侧面上装裱3种不同的透明中国山水画,相邻区域的中国山水画不同,则不同的装裱方案数是