题目内容
若p:m2+2m-3≤0;q:函数f(x)=ex-mx(e为自然对数的底数)在区间(0,+∞)上为增函数,则p是q的 条件(请填:“充分不必要,必要不充分,充分必要,既不充分也不必要”中的一个)
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分条件和必要条件的定义,结合函数单调性的性质,即可得到结论.
解答:
解:由m2+2m-3≤0解得-3≤x≤1,即p:-3≤x≤1.
若f(x)=ex-mx(e为自然对数的底数)在区间(0,+∞)上为增函数,
则f′(x)=ex-m≥0,在区间(0,+∞)上恒成立,即m≤ex在区间(0,+∞)上恒成立,
即m≤1,
故p是q的充分不必要条件,
故答案为:充分不必要.
若f(x)=ex-mx(e为自然对数的底数)在区间(0,+∞)上为增函数,
则f′(x)=ex-m≥0,在区间(0,+∞)上恒成立,即m≤ex在区间(0,+∞)上恒成立,
即m≤1,
故p是q的充分不必要条件,
故答案为:充分不必要.
点评:本题主要考查充分条件和必要条件的应用,利用不等式的性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数z=
-
的虚部为( )
| 1+i |
| i |
| i |
| 1+i |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
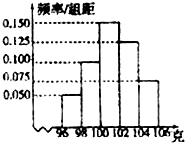 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是