题目内容
11.设函数f(x)=|x-a|+|x|.(Ⅰ)若a=1,解不等式f(x)>2;
(Ⅱ)若存在x∈R,使得不等式f(x)$≤\frac{{t}^{2}+3}{t+1}$对任意t>-1恒成立,求实数a的取值范围.
分析 (Ⅰ)把a=1,代入不等式f(x)>2,利用绝对值的几何意义得答案;
(Ⅱ)利用不等式求出$\frac{{t}^{2}+3}{t+1}$在t>-1时的最小值,转化为存在x∈R,使得不等式f(x)≤2成立,进一步借助于绝对值的几何意义求得实数a的取值范围.
解答 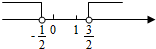 解:(Ⅰ)当a=1,f(x)=|x-1|+|x|.
解:(Ⅰ)当a=1,f(x)=|x-1|+|x|.
不等式f(x)>2化为|x-1|+|x|>2.
如图,由绝对值的几何意义可得:
(Ⅱ)当t>-1时,t+1>0,
$\frac{{t}^{2}+3}{t+1}=\frac{(t+1)^{2}-2(t+1)+4}{t+1}$=$(t+1)+\frac{4}{t+1}-2≥2\sqrt{(t+1)•\frac{4}{t+1}}-2=2$.
当且仅当t+1=$\frac{4}{t+1}$,即t=1时取等号;
若存在x∈R,使得不等式f(x)$≤\frac{{t}^{2}+3}{t+1}$对任意t>-1恒成立,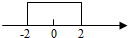
即存在x∈R,使得不等式f(x)≤2成立.
∴在x∈R,使|x-a|+|x|≤2成立.
如图,由绝对值的几何意义可得:
-2≤a≤2.
点评 本题考查函数恒成立问题,考查了绝对值不等式的解法,正确理解、运用绝对值的几何意义是解答该题的关键,是中档题.

练习册系列答案
相关题目
1.已知$\overrightarrow i$和$\overrightarrow j$是互相垂直的单位向量,向量$\overrightarrow{a_n}$满足:$\overrightarrow i•\overrightarrow{a_n}=n$,$\overrightarrow j•\overrightarrow{a_n}=2n+1$,n∈N*,设θn为$\overrightarrow i$和$\overrightarrow{a_n}$的夹角,则( )
| A. | θn随着n的增大而增大 | B. | θn随着n的增大而减小 | ||
| C. | 随着n的增大,θn先增大后减小 | D. | 随着n的增大,θn先减小后增大 |
3.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出下面的表格:
由于粗心,他算错了其中一个y值,则这个错误的数值时( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
| A. | -11 | B. | -2 | C. | 1 | D. | -5 |