题目内容
已知三点A(-
,0),B(2,0),P(sin(2x-
),cos(2x-
))(
≤x≤
)
(1)求△ABP面积的最小值;
(2)在(1)的条件下,求∠ABP的大小.
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 12 |
| π |
| 4 |
(1)求△ABP面积的最小值;
(2)在(1)的条件下,求∠ABP的大小.
考点:三角函数中的恒等变换应用
专题:计算题
分析:(1)根据x的范围,判断出p点在x轴上方,列出面积的表达式,根据余弦函数的单调性求得其最小值.
(2)求出|OP|、|PB|、|OB|的长度,利用勾股定理判断△OPB为直角三角形,进而求得∠ABP.
(2)求出|OP|、|PB|、|OB|的长度,利用勾股定理判断△OPB为直角三角形,进而求得∠ABP.
解答:
解:(1)∵
≤x≤
,
∴-
≤2x-
≤
,
∴cos(2x-
)>0,即点P在x轴上方,
∴S△ABP=
•
•cos(2x-
)=
cos(2x-
),
∵-
≤2x-
≤
∴S△ABP≥
,当且仅当x=
时,△ABP的面积的最小值为
.
(2)当△ABP的面积取最小值时,点P(
,
),
∴|OP|=
=1,|PB|=
=
,|OB|=2
∴|OP|2+|PB|2=|OB|2,即△OPB为直角三角形,且|OP|=1,|OB|=2,
∴∠ABP=
| π |
| 12 |
| π |
| 4 |
∴-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∴cos(2x-
| π |
| 3 |
∴S△ABP=
| 1 |
| 2 |
| 5 |
| 2 |
| π |
| 3 |
| 5 |
| 4 |
| π |
| 3 |
∵-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∴S△ABP≥
| 5 |
| 8 |
| 3 |
| π |
| 4 |
| 5 |
| 8 |
| 3 |
(2)当△ABP的面积取最小值时,点P(
| 1 |
| 2 |
| ||
| 2 |
∴|OP|=
(
|
(
|
| 3 |
∴|OP|2+|PB|2=|OB|2,即△OPB为直角三角形,且|OP|=1,|OB|=2,
∴∠ABP=
| π |
| 6 |
点评:本题主要考查了三角函数中的恒等变换的应用.注重了对三角函数基础知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设全集U是实数集R,集合M={x|x2≥2x},N={x|log2(x-1)≤0},则M∩N=( )
| A、{1,2} |
| B、{ 2 } |
| C、{1} |
| D、[1,2] |
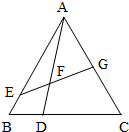 如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC,设
如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC,设