题目内容
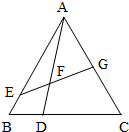如图，在△ABC中，已知CD=2DB，BA=5BE，AF=mAD，AG=tAC，设| 1 |
| 3 |
| 1 |
| 2 |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：根据三点共线的，向量的加减运算，代入计算即可．
解答：
解：根据题意得，
=
，
=
，
=
，①
∵
=2
，
∴
-
=2(
-
)，②
将①代入②，化简得，
=
+
，
由于E，F，G三点共线，
∴
+
=1，
∴t=
，
∵
≤m≤
，
∴
≤t≤
．
| AB |
| 5 |
| 4 |
| AE |
| AC |
| 1 |
| t |
| AG |
| AD |
| 1 |
| m |
| AF |
∵
| CD |
| DB |
∴
| AD |
| AC |
| AB |
| AD |
将①代入②，化简得，
| AF |
| 5m |
| 6 |
| AE |
| m |
| 3t |
| AG |
由于E，F，G三点共线，
∴
| 5m |
| 6 |
| m |
| 3t |
∴t=
| 2m |
| 6-5m |
∵
| 1 |
| 3 |
| 1 |
| 2 |
∴
| 2 |
| 13 |
| 2 |
| 7 |
点评：本题考查了向量的加减混合运算，关键是E，F，G三点共线，得到t含有m的表达式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
长方体AC1中，AB=BC=2，AA1=