题目内容

5．《数学选修1-2》的知识结构图如图所示，则“直接证明与间接证明”的“上位”要素是（　　）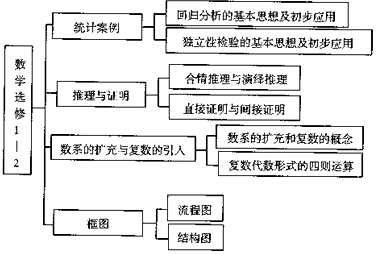
A．推理与证明B．统计案例
C．数系的扩充与复数的引入D．框图

分析 对所画知识结构图的每一部分有一个深刻的理解，从头到尾抓住主要脉络进行分解，即可得出结论．

解答 解：根据该知识结构图知，“直接证明与间接证明”是建立在“推理与证明”的下一步，
∴“直接证明与间接照明”的“上位”要素是“推理与证明”．
故选：A．

点评 本题主要考查了知识结构图的应用问题，是基础题．

练习册系列答案
相关题目
17．在ABC中，角A，B，C的对边分别为a，b，c，若△ABC为锐角三角形，且满足sinB（1+2cosC）=2sinAcosC+cosAsinC，则下列等式成立的是（　　）
A．a=2bB．b=2aC．A=2BD．B=2A
18．电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广告．已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播放时长、收视人次如下表所示：
连续剧播放时长（分钟）广告播放时长（分钟）收视人次（万）
甲70560
乙60525
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟，广告的总播放时间不少于30分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的2倍．分别用x，y表示每周计划播出的甲、乙两套连续剧的次数．
（I）用x，y列出满足题目条件的数学关系式，并画出相应的平面区域；
（II）问电视台每周播出甲、乙两套连续剧各多少次，才能使总收视人次最多？
13．已知函数$f（x）=\frac{1}{2}a{x^2}-（{2a+1}）x+2lnx（{x∈R}）$
（Ⅰ）若曲线y=f（x）在x=1和x=3处的切线互相平行，求a的值；
（Ⅱ）求f（x）的单调区间．
20．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，椭圆的四个顶点所围成菱形的面积为4
（Ⅰ）求椭圆的方程；
（Ⅱ）四边形ABCD的顶点在椭圆C上，且对角线AC，BD均过坐标原点O，若kAC•kBD=-$\frac{1}{4}$
（i）求$\overrightarrow{OA}$•$\overrightarrow{OB}$的范围；（ii）求四边形ABCD的面积．
10．在△ABC中，角A、B、C所对的边分别为a，b，c，已知a=1，b=$\sqrt{3}$，A=30°，B为锐角，那么角A：B：C的比值为（　　）
A．1：1：3B．1：2：3C．1：3：2D．1：4：1
17．某几何体三视图如图所示，则该几何体体积为（　　）
A．6B．7C．8D．9
14．已知函数f（x）=x3+ax2+b的图象上一点P（1，0），且在P点处的切线与直线3x+y=0平行．
（1）求函数f（x）的解析式；
（2）求函数f（x）在区间[0，t]（0＜t＜3）上的最大值和最小值；
（3）在（1）的结论下，关于x的方程f（x）=c在区间[1，3]上恰有两个相异的实根，求实数c
的取值范围．
15．某算法的伪代码如图所示，如果输入的x值为32，则输出的y值为5． 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网