题目内容
14.已知函数f(x)=x3+ax2+b的图象上一点P(1,0),且在P点处的切线与直线3x+y=0平行.(1)求函数f(x)的解析式;
(2)求函数f(x)在区间[0,t](0<t<3)上的最大值和最小值;
(3)在(1)的结论下,关于x的方程f(x)=c在区间[1,3]上恰有两个相异的实根,求实数c
的取值范围.
分析 (1)利用导数的几何意义求出a,根据函数过(1,0)点,求出b,即可求出函数f(x)的解析式;
(2)求导数,分类讨论,确定函数的单调性,即可求出函数f(x)在区间[0,t](0<t<3)上的最大值和最小值;
(3)构造函数,研究构造函数的性质尤其是单调性,列出该方程有两个相异的实根的不等式组,求出实数a的取值范围.
解答 解:(1)因为f′(x)=3x2+2ax,曲线在P(1,0)处的切线斜率为f′(1)=3+2a,
即3+2a=-3,
所以a=-3;
又因为函数过(1,0)点,
即-2+b=0,
所以b=2,
所以f(x)=x3-3x2+2
(2)由f(x)=x3-3x2+2,f′(x)=3x2-6x,
令f′(x)=0,可得x=0或x=2,
①当0<t≤2时,在区间(0,t)上f′(x)<0,
可得f(x)在[0,t]上是减函数,
所以f(x)max=f(0)=2,
f(x)min=f(t)=t3-3t2+2;
②当2<t<3时,当x变化时,f′(x)、f(x)的变化情况见下表:
| x | 0 | (0,2) | 2 | (2,t) | t |
| f′(x) | 0 | - | 0 | + | + |
| f(x) | 2 | 递减 | -2 | 递增 | t3-3t2+2 |
f(x)max为f(0)与f(t)中较大的一个,
f(t)-f(0)=t3-3t2=t2(t-3)<0,
所以f(x)max=f(0)=2,
综上,函数f(x)在区间[0,t](0<t<3)上的最大值是2,最小值是-2.
(3)令g(x)=f(x)-c=x3-3x2+2-c,g′(x)=3x2-6x=3x(x-2).
在x∈上,g′(x)>0.要使g(x)=0在上恰有两个相异的实根,
则$\left\{\begin{array}{l}g(1)≥0\\ g(2)<0\\ g(3)≥0\end{array}\right.$,解得-2<c≤0.
点评 本题考查导数的工具作用,考查学生利用导数研究函数的单调性的知识.考查学生对方程、函数、不等式的综合问题的转化与化归思想,将方程的根的问题转化为函数的图象交点问题,属于综合题型.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
5.《数学选修1-2》的知识结构图如图所示,则“直接证明与间接证明”的“上位”要素是( )
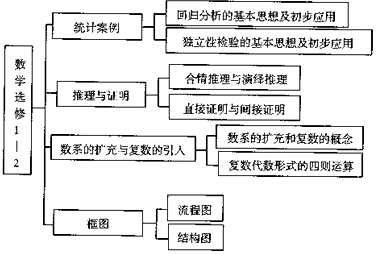

| A. | 推理与证明 | B. | 统计案例 | ||
| C. | 数系的扩充与复数的引入 | D. | 框图 |
2.某公司的组织结构图如图所示,其中技术服务部的直接领导是( )

| A. | 董事长 | B. | 监事会 | C. | 总经理 | D. | 总工程师 |
19.已知函数$f(x)=\left\{\begin{array}{l}({4a-3})x+2a-4,x≤t\\ 2{x^3}-6x,x>t\end{array}\right.$,无论t取何值,函数f(x)在R上总是不单调,则实数a的取值范围是( )
| A. | (-∞,1) | B. | $[{\frac{1}{4},+∞})$ | C. | $[{\frac{3}{4},+∞})$ | D. | $({-∞,\frac{3}{4}}]$ |
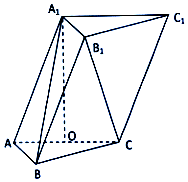 如图,在三棱柱ABC-A1B1C1中,$AB=BC=\sqrt{5},AC=2$且点A1在底面ABC上的射影O恰是线段AC的中点,$A{A_1}=\sqrt{5}$.
如图,在三棱柱ABC-A1B1C1中,$AB=BC=\sqrt{5},AC=2$且点A1在底面ABC上的射影O恰是线段AC的中点,$A{A_1}=\sqrt{5}$.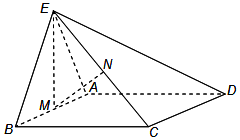 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.