题目内容

17．在ABC中，角A，B，C的对边分别为a，b，c，若△ABC为锐角三角形，且满足sinB（1+2cosC）=2sinAcosC+cosAsinC，则下列等式成立的是（　　）
A．a=2bB．b=2aC．A=2BD．B=2A

分析 利用两角和与差的三角函数化简等式右侧，然后化简通过正弦定理推出结果即可．

解答 解：在ABC中，角A，B，C的对边分别为a，b，c，满足sinB（1+2cosC）=2sinAcosC+cosAsinC=sinAcosC+sin（A+C）=sinAcosC+sinB，
可得：2sinBcosC=sinAcosC，因为△ABC为锐角三角形，所以2sinB=sinA，
由正弦定理可得：2b=a．
故选：A．

点评 本题考查两角和与差的三角函数，正弦定理的应用，考查计算能力．

练习册系列答案
相关题目
3．我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（　　）
A．1盏B．3盏C．5盏D．9盏
8．将函数y=sin（2x-$\frac{π}{3}$）的图象向左平移$\frac{π}{4}$个单位长度，所得函数图象的一条对称轴方程是（　　）
A．x=$\frac{2}{3}$πB．x=-$\frac{1}{12}$πC．x=$\frac{1}{3}$πD．x=$\frac{5}{12}$π
5．设函数f（x）=（1-x2）ex．
（1）讨论f（x）的单调性；
（2）当x≥0时，f（x）≤ax+1，求a的取值范围．
12．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y+3≤0}\\{3x+y+5≤0}\\{x+3≥0}\end{array}\right.$，则z=x+2y的最大值是（　　）
A．0B．2C．5D．6
2．设函数f（x）=sin（ωx-$\frac{π}{6}$）+sin（ωx-$\frac{π}{2}$），其中0＜ω＜3，已知f（$\frac{π}{6}$）=0．
（Ⅰ）求ω；
（Ⅱ）将函数y=f（x）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移$\frac{π}{4}$个单位，得到函数y=g（x）的图象，求g（x）在[-$\frac{π}{4}$，$\frac{3π}{4}$]上的最小值．
9．设集合A={1，2，6}，B={2，4}，C={x∈R|-1≤x≤5}，则（A∪B）∩C=（　　）
A．{2}B．{1，2，4}C．{1，2，4，5}D．{x∈R|-1≤x≤5}
6．已知{an}为等差数列，前n项和为Sn（n∈N+），{bn}是首项为2的等比数列，且公比大于0，b2+b3=12，b3=a4-2a1，S11=11b4．
（Ⅰ）求{an}和{bn}的通项公式；
（Ⅱ）求数列{a2nb2n-1}的前n项和（n∈N+）．
5．《数学选修1-2》的知识结构图如图所示，则“直接证明与间接证明”的“上位”要素是（　　）
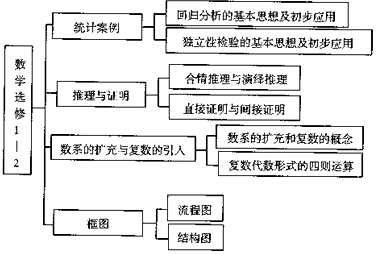
A．推理与证明B．统计案例
C．数系的扩充与复数的引入D．框图

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网