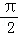题目内容
一只半径为R的球放在桌面上,桌面上一点A的正上方相距( +1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为 .
+1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为 .

【解析】
试题分析:根据圆曲线的第一定义,作出过圆锥的轴与椭圆长轴AA′的截面,可得直角三角形AOA′,结合已知求出椭圆的a值,再根据椭圆的几何性质,求出c,即可求出椭圆的离心率.
【解析】
如图是过圆锥的轴与椭圆长轴AA′的截面,
ED两点为过点O引圆D的两条切线与圆D的切点,
∵OA=( +1)R,
+1)R,
故在Rt△OBE中,
OE= R,BE=R,
R,BE=R,
则tan∠EOB= ,
,
即∠EOB=30°,
故∠EOB=60°,即∠AOA′=60°,
故AA′=2a= OA=(3+
OA=(3+ )R,即a=
)R,即a= ,
,

根据圆锥曲线的定义,
可得球与长轴AA′的切点是椭圆的焦点F,
根据椭圆的几何性质,AF是焦点到长轴顶点的距离AF=a﹣c=R,
∴c= =
= a,
a,
所求椭圆的离心率e= =
= ,
,
故答案为:

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
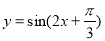 在区间
在区间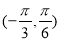 内单调递增
内单调递增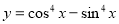 的最小正周期为
的最小正周期为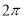
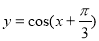 的图像是关于点
的图像是关于点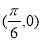 成中心对称的图形
成中心对称的图形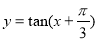 的图像是关于直线
的图像是关于直线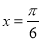 成轴对称的图形
成轴对称的图形 的图像向右平移
的图像向右平移 个单位,再向上平移
个单位,再向上平移 个单位,
个单位,


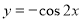
 的所有数按照从大到小的原则写成如下数表:
的所有数按照从大到小的原则写成如下数表: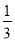


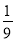
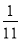






 行有
行有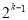 个数,第
个数,第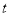 行的第
行的第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则
 中,
中, ,且对任意的正整数
,且对任意的正整数 都有
都有 ,则若
,则若 时,
时, _________.
_________.
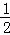 B.
B.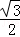 C.
C.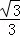 D.
D.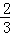
 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )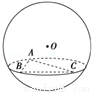
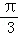 B.π C.
B.π C.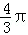 D.2π
D.2π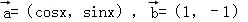 ,将函数
,将函数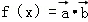 的图象按向量
的图象按向量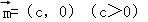 平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )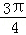 B.π C.
B.π C.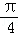 D.
D.