题目内容
曲线f(x)=lnx+2x在点(1,f(1))处的切线方程是( )
A.3x﹣y+1=0 B.3x﹣y﹣1=0 C.3x+y﹣1=0 D.3x﹣y﹣5=0
B
【解析】
试题分析:先要求出在给定点的函数值,然后再求出给定点的导数值.
将所求代入点斜式方程即可.
【解析】
对f(x)=lnx+2x求导,得
f′(x)= +2.
+2.
故在点(1,f(1))处可以得到
f(1)=ln1+2=2,
f′(1)=1+2=3.
所以在点(1,f(1))处的切线方程是:
y﹣f(1)=f′(1)(x﹣1),代入化简可得,
3x﹣y﹣1=0.
故选B.

练习册系列答案
相关题目
 的所有数按照从大到小的原则写成如下数表:
的所有数按照从大到小的原则写成如下数表: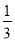


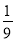
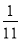






 行有
行有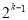 个数,第
个数,第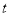 行的第
行的第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则
 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )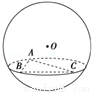
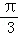 B.π C.
B.π C.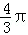 D.2π
D.2π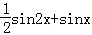 ,则f′(x)是( )
,则f′(x)是( ) ,x<0时,f′(x)=﹣
,x<0时,f′(x)=﹣
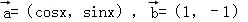 ,将函数
,将函数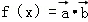 的图象按向量
的图象按向量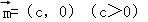 平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )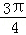 B.π C.
B.π C.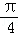 D.
D.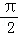
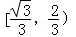 B.
B.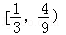 C.
C.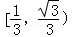 D.
D.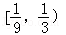
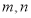 .
.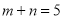 ”的概率;
”的概率;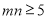 ”的概率.
”的概率.