题目内容
双曲线ky2-8kx2=8的一个焦点为(0,3),则该双曲线渐近线方程为 (填一般方程)
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据双曲线的焦点坐标,求出k,即可求出双曲线的渐近线方程.
解答:
解:∵双曲线ky2-8kx2=8的一个焦点为(0,3),
∴双曲线ky2-8kx2=8的标准方程是
-
=1,
则a2=
,b2=
,
则a2+b2═
+
=
=32=9,解得k=1,
即双曲线的标准方程为
-x2=1,
则对应的渐近线方程为±2
x-y=0,
故答案为:±2
x-y=0
∴双曲线ky2-8kx2=8的标准方程是
| y2 | ||
|
| x2 | ||
|
则a2=
| 8 |
| k |
| 1 |
| k |
则a2+b2═
| 8 |
| k |
| 1 |
| k |
| 9 |
| k |
即双曲线的标准方程为
| y2 |
| 8 |
则对应的渐近线方程为±2
| 2 |
故答案为:±2
| 2 |
点评:本题主要考查双曲线的方程和性质,根据条件求出k的值是解决本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
设变量x,y满足约束条件:
,则目标函数z=x-y的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
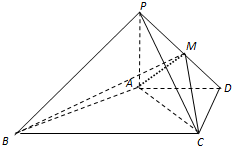 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=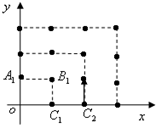 2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在A1(0,1)点,第二棵树在B1(1,1)点,第三棵树在C1(,0)点,第四棵树在C2(2,0)点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是
2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在A1(0,1)点,第二棵树在B1(1,1)点,第三棵树在C1(,0)点,第四棵树在C2(2,0)点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是