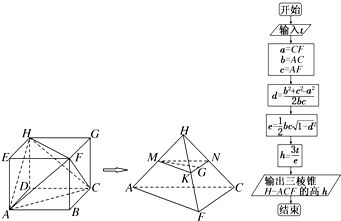
题目内容
已知凼数f(x)=2cos2x-2sinxcosx+1
(1)求方程f(x)-1=0在x∈(0,π)内的所有解的和;
(2)把凼数y=f(x)的图象向左平移m(m>0)个单位,使所得函数的图象关于点(0,2)对称,求m的最小值.
(1)求方程f(x)-1=0在x∈(0,π)内的所有解的和;
(2)把凼数y=f(x)的图象向左平移m(m>0)个单位,使所得函数的图象关于点(0,2)对称,求m的最小值.
考点:两角和与差的正弦函数,函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的求值,三角函数的图像与性质
分析:(1)利用二倍角公式对函数f(x)的解析式化简整理,根据f(x)-1=0,求得cos(2x+
)=-
,进而求得x,则可得在x∈(0,π)内的所有解,进而求得之和.
(2)设y=f(x)的图象向左平移m个单位,得到函数g(x)的图象,则可知g(x)的解析式,根据函数的图象关于(0,2)对称,进而求得m的集合,进而求得m的最小值.
| π |
| 4 |
| ||
| 2 |
(2)设y=f(x)的图象向左平移m个单位,得到函数g(x)的图象,则可知g(x)的解析式,根据函数的图象关于(0,2)对称,进而求得m的集合,进而求得m的最小值.
解答:
解:(1)由题设得f(x)=-sin2x+1+cos2x+1=
cos(2x+
)+2,
∵f(x)-1=0,
∴
cos(2x+
)+2=1,
∴cos(2x+
)=-
,
由2x+
=2kπ+
或2kπ+
π,k∈Z.得x=kπ+
或kπ+
,
∵x∈(0,π)
∴x1=
,x2=
,
∴x1+x2=
;
(2)设y=f(x)的图象向左平移m个单位,得到函数g(x)的图象,
则g(x)=cos(2x+
+2m)+2,
∵y=g(x)的图象关于点(0,2)对称,
∴2m+
=kπ+
,k∈Z,
∴2m=kπ+
,m=
+
,k∈Z,
∵m>0,∴当k=0时,m取得最小值
.
| 2 |
| π |
| 4 |
∵f(x)-1=0,
∴
| 2 |
| π |
| 4 |
∴cos(2x+
| π |
| 4 |
| ||
| 2 |
由2x+
| π |
| 4 |
| 3π |
| 4 |
| 5 |
| 4 |
| π |
| 4 |
| π |
| 2 |
∵x∈(0,π)
∴x1=
| π |
| 4 |
| π |
| 2 |
∴x1+x2=
| 3π |
| 4 |
(2)设y=f(x)的图象向左平移m个单位,得到函数g(x)的图象,
则g(x)=cos(2x+
| π |
| 4 |
∵y=g(x)的图象关于点(0,2)对称,
∴2m+
| π |
| 4 |
| π |
| 2 |
∴2m=kπ+
| π |
| 4 |
| kπ |
| 2 |
| π |
| 8 |
∵m>0,∴当k=0时,m取得最小值
| π |
| 8 |
点评:本题主要考查了二倍角公式,三角函数图象的平移,及对称性.考查了学生综合把握三角函数知识的能力.

练习册系列答案
相关题目
不等式|x|>3的解集为( )
| A、{x|x>3} |
| B、{x|x>±3} |
| C、{x|-3<x<3} |
| D、{x|x<-3或x>3} |
函数f(x)=ln(x+1)•tanx的图象可能是( )
A、 |
B、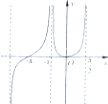 |
C、 |
D、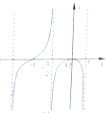 |