题目内容
已知实数x,y满足x2+y2+xy=1,则x+2y的最大值为 .
考点:基本不等式
专题:不等式的解法及应用
分析:x+2y=m,则x=m-2y代入x2+y2+xy=1,可得3y2-3my+m2-1=0,利用△≥0,解出即可.
解答:
解:设x+2y=m,则x=m-2y代入x2+y2+xy=1,可得3y2-3my+m2-1=0,
∴△=9m2-12(m2-1)≥0,
解得-2≤m≤2,
∴x+2y的最大值为2.
故答案为:2.
∴△=9m2-12(m2-1)≥0,
解得-2≤m≤2,
∴x+2y的最大值为2.
故答案为:2.
点评:本题考查了一元二次方程的实数根与判别式的关系、一元二次不等式的解法,属于基础题.

练习册系列答案
相关题目
sin(-1560°)的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
下列说法正确的是( )
| A、一个平面的面积可以是16cm2 |
| B、空间三点可以确定一个平面 |
| C、平面α与平面β相交于线段AB |
| D、两条相交直线可以确定一个平面 |
直线x+y=1和圆:x2+y2-6x+8y-24=0的位置关系是( )
| A、相切 | B、相交 | C、相离 | D、不确定 |
已知x∈(0,1)时,函数f(x)=
的最小值为b,若定义在R上的函数g(x)满足:对任意m,n∈R都有g(m+n)=g(m)+g(n)+b,则下列结论正确的是( )
| 1+2x2 | ||
2x
|
| A、g(x)-1是奇函数 | ||
| B、g(x)+1是奇函数 | ||
C、g(x)-
| ||
D、g(x)-
|
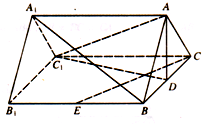 如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.