题目内容
已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:
+
=1(a>b>0)的右焦点F和上顶点B,则椭圆Γ的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由椭圆方程求出F、B的坐标,把坐标代入圆的方程求出b、c,由a2=b2+c2求出a,再求出椭圆C的离心率.
解答:
解:由题意得,椭圆的右焦点F为(c,0)、上顶点B为(0,b),
因为圆(x-1)2+(y-1)2=2经过右焦点F和上顶点 B,
所以
,解得b=c=2,
则a2=b2+c2=8,解得a=2
,
所以椭圆C的离心率e=
=
=
,
故答案为:
.
因为圆(x-1)2+(y-1)2=2经过右焦点F和上顶点 B,
所以
|
则a2=b2+c2=8,解得a=2
| 2 |
所以椭圆C的离心率e=
| c |
| a |
| 2 | ||
2
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查椭圆的简单几何性质,以及a、b、c的关系,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
sin(-1560°)的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
设A={x|-3≤x≤3},B={y|y=-x2+t},若A∩B=∅,则实数t的取值范围是( )
| A、t<-3 | B、t≤-3 |
| C、t>3 | D、t≥3 |
设二次函数f(x)=ax2+bx+c的导函数为f′(x),对?x∈R,不等式f(x)≥f′(x)恒成立,则
的最大值为( )
| b2 |
| a2+2c2 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知向量
,
的模分别为1,2,它们的夹角为60°,则向量
-
与-4
+
的夹角为( )
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| A、60° | B、120° |
| C、30° | D、150° |
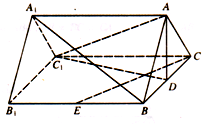 如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.