题目内容
已知向量
=(cosax,sinax),
=(
cosax,-cosax),其中a>0,若f(x)=
•
的图象与y=m(m>0)相切,且切点横坐标成公差为π的等差数列.
(Ⅰ)求a和m的值;
(Ⅱ)在△ABC中,若f(
)=
,且BC=4,求△ABC面积的最大值.
| a |
| b |
| 3 |
| a |
| b |
(Ⅰ)求a和m的值;
(Ⅱ)在△ABC中,若f(
| A |
| 2 |
| ||
| 2 |
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:等差数列与等比数列,解三角形,平面向量及应用
分析:(Ⅰ)运用向量的数量积的坐标表示和二倍角公式及两角和的余弦公式,化简f(x),再由相切可得m为f(x)的最大值,再由等差数列的通项公式可得a=1;
(Ⅱ)由f(x)的解析式,可得A,再由余弦定理和基本不等式,可得bc的最大值为16,运用三角形的面积公式计算即可得到所求最大值.
(Ⅱ)由f(x)的解析式,可得A,再由余弦定理和基本不等式,可得bc的最大值为16,运用三角形的面积公式计算即可得到所求最大值.
解答:
解:(Ⅰ)由于向量
=(cosax,sinax),
=(
cosax,-cosax),其中a>0,
则f(x)=
•
=
cos2ax-sinaxcosax=
(1+cos2ax)-
sin2ax=
+cos(2ax+
),
若f(x)图象与y=m(m>0)相切,则m为f(x)的最大值,即为1+
;
又切点横坐标成公差为π的等差数列,由2ax+
=2kπ,即有x=
π-
,k∈Z,
即有a=1.
(Ⅱ)在△ABC中,若f(
)=
,
则
+cos(A+
)=
,
即有cos(A+
)=0,
由A为三角形的内角,则A+
=
,
即A=
,
且BC=4,由余弦定理可得42=b2+c2-2bccosA,
即有16=b2+c2-bc≥2bc-bc,即有bc≤16,
则△ABC面积S=
bcsinA=
bc≤4
.
当且仅当b=c=4,三角形的面积取得最大值4
.
| a |
| b |
| 3 |
则f(x)=
| a |
| b |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
若f(x)图象与y=m(m>0)相切,则m为f(x)的最大值,即为1+
| ||
| 2 |
又切点横坐标成公差为π的等差数列,由2ax+
| π |
| 6 |
| k |
| a |
| π |
| 12 |
即有a=1.
(Ⅱ)在△ABC中,若f(
| A |
| 2 |
| ||
| 2 |
则
| ||
| 2 |
| π |
| 6 |
| ||
| 2 |
即有cos(A+
| π |
| 6 |
由A为三角形的内角,则A+
| π |
| 6 |
| π |
| 2 |
即A=
| π |
| 3 |
且BC=4,由余弦定理可得42=b2+c2-2bccosA,
即有16=b2+c2-bc≥2bc-bc,即有bc≤16,
则△ABC面积S=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
当且仅当b=c=4,三角形的面积取得最大值4
| 3 |
点评:本题主要考查向量的数量积的坐标运算和三角恒等变换、三角函数的性质等基础知识,同时考查三角形的余弦定理和面积公式的运用,运用基本不等式求最值是解题的关键.

练习册系列答案
相关题目
设函数f(x)=2cos2x+
sin2x,x∈R,则下列结论正确的是( )
| 3 |
A、f(x)的图象关于直线x=
| ||
| B、f(x)的最大值是2 | ||
C、f(x)在[0,
| ||
D、f(x)的图象关于点(
|
若函数f(x)=|x+1|+|2x-a|的最小值为3,则实数a的值为( )
| A、4或-8 | B、-5或-8 |
| C、1或-5 | D、1或4 |
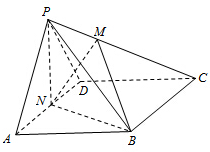 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD