题目内容
设P是圆x2+y2=4上的任意一点，过P作x轴的垂线段PD，D为垂足，M是线段PD上的点，且满足|DM|=m|PD|（0＜m＜1），当点P在圆上运动时，记M的轨迹为曲线C．
（1）求曲线C的方程；
（2）过曲线C的左焦点F作斜率为
的直线l交曲线C于A、B两点，点Q满足
+
+
=
，是否存在实数m，使得点Q在曲线C上，若存在，求出m的值，若不存在，请说明理由．
（1）求曲线C的方程；
（2）过曲线C的左焦点F作斜率为
| ||
| 2 |
| OA |
| OB |
| OQ |
| 0 |
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）由|DM|=m|PD|，确定M，P的坐标，代入圆的方程，即可求曲线C的方程；
（2）设出直线l的方程，代入椭圆方程，利用韦达定理，结合
+
+
=
，求出Q的坐标，代入椭圆方程，即可得出结论．
（2）设出直线l的方程，代入椭圆方程，利用韦达定理，结合
| OA |
| OB |
| OQ |
| 0 |
解答：
解：（1）如图设M（x，y）、P（x0，y0），则由|DM|=m|PD|（0＜m＜1）得
x=x0，|y|=m|y0|，即
∵x02+y02=4，∴
+
=1，即为曲线C的方程；…6′
（2）设c=2
，则F(-c，0)，l：y=
(x+c)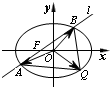
由
得：（2m2+1）x2+2cx+4-12m2=0…8′
设A（x1，y1）、B（x2，y2）．
则x1+x2=-
，x1x2=
．
∴y1+y2=
(x1+x2+2c)，…9′
∵
=-(
+
)=-(x1+x2，y1+y2)=(
，
)
即Q点坐标为(
，
)，将Q点代入
+
=1，得m=
．
∴存在当m=
时，Q点在曲线C上．…13′
解：（1）如图设M（x，y）、P（x0，y0），则由|DM|=m|PD|（0＜m＜1）得x=x0，|y|=m|y0|，即
|
∵x02+y02=4，∴
| x2 |
| 4 |
| y2 |
| 4m2 |
（2）设c=2
| 1-m2 |
| ||
| 2 |
由
|
设A（x1，y1）、B（x2，y2）．
则x1+x2=-
| 2c |
| 2m2+1 |
| 4-12m2 |
| 2m2+1 |
∴y1+y2=
| ||
| 2 |
∵
| OQ |
| OA |
| OB |
| 2c |
| 2m2+1 |
-2
| ||
| 2m2+1 |
即Q点坐标为(
| 2c |
| 2m2+1 |
-2
| ||
| 2m2+1 |
| x2 |
| 4 |
| y2 |
| 4m2 |
| ||
| 2 |
∴存在当m=
| ||
| 2 |
点评：本题考查椭圆方程，考查直线与椭圆的位置关系，考查向量知识的运用，考查学生分析解决问题的能力，正确运用代入法是关键．
练习册系列答案
相关题目
已知两条直线a，b，两个平面α，β．给出下面四个命题：
①a∥b，a∥α⇒b∥α；
②a?α，b⊥β，α∥β⇒a⊥b；
③a⊥α，a∥b，b∥β⇒α∥β；
④α∥β，a∥b，a⊥α⇒b⊥β．
其中正确的命题序号为（ ）
①a∥b，a∥α⇒b∥α；
②a?α，b⊥β，α∥β⇒a⊥b；
③a⊥α，a∥b，b∥β⇒α∥β；
④α∥β，a∥b，a⊥α⇒b⊥β．
其中正确的命题序号为（ ）
| A、①② | B、②③ | C、①④ | D、②④ |
设等差数列{an}的前n项和为Sn，若S7＞S8＞S6，则满足Sn•Sn+1＜0的正整数n的值为（ ）
| A、11 | B、12 | C、13 | D、14 |
在直角坐标系中，直线y=
x+2的倾斜角是（ ）
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设a，b，c∈R，且a+b+c=2，a2+b2+c2=12，则c的最大值和最小值的差为（ ）
| A、2 | ||
B、
| ||
C、
| ||
D、
|
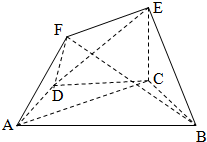如图，在多面体ABCDEF中，底面ABCD是梯形，且满足AD=DC=CB=
（文）已知中心在原点O，左焦点为F1（-1，0）的椭圆C的左顶点为A，上顶点为B，F1到直线AB的距离为