题目内容
已知椭圆的长轴长是短轴长的2倍,且焦点在x轴上,且椭圆截直线y=x+2所得线段AB的长为16
.
(1)求椭圆的方程;
(2)求△OAB的面积.
| ||
| 5 |
(1)求椭圆的方程;
(2)求△OAB的面积.
考点:椭圆的简单性质,椭圆的标准方程
专题:计算题,圆锥曲线中的最值与范围问题
分析:(1)由题意设椭圆的方程为
+
=1,可得a=2b,与直线方程联立,利用韦达定理简化运算,从而椭圆的方程,
(2)求点O到直线y=x+2的距离d=
=
,即高,从而求面积.
| x2 |
| a2 |
| y2 |
| b2 |
(2)求点O到直线y=x+2的距离d=
| 2 | ||
|
| 2 |
解答:
解:(1)设椭圆的方程为
+
=1,
则由题意可得,a=2b,
故
+
=1可化为x2+4y2=4b2,
与直线y=x+2联立消y化简可得,
5x2+16x+16-4b2=0,
设点A(a,b),B(m,n),
则由椭圆截直线y=x+2所得线段AB的长为16
可知,
|a-m|=
,
又∵a+m=-
,
故16-4b2=0,
则b=2,
故椭圆的方程为
+
=1.
(2)∵点O到直线y=x+2的距离d=
=
,
∴S△OAB=
×16
×
=
.
| x2 |
| a2 |
| y2 |
| b2 |
则由题意可得,a=2b,
故
| x2 |
| a2 |
| y2 |
| b2 |
与直线y=x+2联立消y化简可得,
5x2+16x+16-4b2=0,
设点A(a,b),B(m,n),
则由椭圆截直线y=x+2所得线段AB的长为16
| ||
| 5 |
|a-m|=
| 16 |
| 5 |
又∵a+m=-
| 16 |
| 5 |
故16-4b2=0,
则b=2,
故椭圆的方程为
| x2 |
| 16 |
| y2 |
| 4 |
(2)∵点O到直线y=x+2的距离d=
| 2 | ||
|
| 2 |
∴S△OAB=
| 1 |
| 2 |
| ||
| 5 |
| 2 |
| 16 |
| 5 |
点评:本题考查了椭圆的方程的求法,属于中档题.

练习册系列答案
相关题目
若异面直线l1,l2的方向向量分别是
=(0,-2,-1),
=(2,0,4),则异面直线l1与l2的夹角的余弦值等于( )
| a |
| b |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
若非零向量
,
,满足|
|=|
|=|
-
|,则
与
-
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
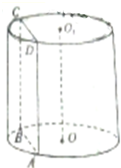 已知圆柱OO1的底面半径为2,高为4.
已知圆柱OO1的底面半径为2,高为4.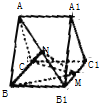 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=