题目内容
在△ABC中，角A，B，C所对应的边分别为a，b，c，则“a≥b”是“sinA≥sinB”的（ ）
| A、充分必要条件 |
| B、充分而非必要条件 |
| C、必要非充分条件 |
| D、非充分非必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义，结合正弦定理即可得到结论．
解答：
解：在三角形中，根据正弦定理可得若“a≥b”则“sinA≥sinB”成立，反之也成立，
即“a≥b”是“sinA≥sinB”的充分且必要条件，
故选：A
即“a≥b”是“sinA≥sinB”的充分且必要条件，
故选：A
点评：本题主要考查充分条件和必要条件的判断，根据正弦定理是解决本题的关键．
练习册系列答案
相关题目
集合A={x|x=2n，n∈Z}，B={y|y=4k，k∈Z}，则A与B的关系为（ ）
| A、A?B | B、A?B |
| C、A=B | D、A∈B |
从1，2，3，4，5，6，7，8，9这9个数字中任取两个数，分别有下列事件：
①恰有一个是奇数和恰有一个是偶数；
②至少有一个是奇数和两个都是奇数；
③至少有一个是奇数和两个都是偶数；
④至少有一个是奇数和至少有一个是偶数．
其中为互斥事件的是（ ）
①恰有一个是奇数和恰有一个是偶数；
②至少有一个是奇数和两个都是奇数；
③至少有一个是奇数和两个都是偶数；
④至少有一个是奇数和至少有一个是偶数．
其中为互斥事件的是（ ）
| A、① | B、②④ | C、③ | D、①③ |
若复数{kn}满足（1-i）z=i，则z在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中，若有
=cos2
，则△ABC的形状是（ ）
| a+b |
| 2b |
| C |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、直角三角形或锐角三角形 |
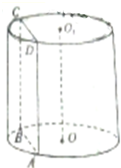已知圆柱OO1的底面半径为2，高为4．