题目内容
已知单位向量
，
的夹角为
，在△ABC中，
=2
+
，
=2
-5
，D是边BC的中点，则|
|等于（ ）
| m |
| n |
| π |
| 3 |
| AB |
| m |
| n |
| AC |
| m |
| n |
| AD |
| A、12 | ||
B、2
| ||
| C、4 | ||
| D、2 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由向量的数量积的定义和性质可得
•
，|
|，|
|和
•
，再由中点的向量表示可得
=
（
+
），再由向量的平方即为模的平方，代入计算即可得到．
| m |
| n |
| AB |
| AC |
| AB |
| AC |
| AD |
| 1 |
| 2 |
| AB |
| AC |
解答：
解：由
•
=1×1×cos
=
，
|
|2=（2
+
）2=4
2+
2+4
•
=4+1+4×
=7，则|
|=
，
|
|2=（2
-5
）2=4
2+25
2-20
•
=4+25-20×
=19，
即有|
|=
，
又
•
=（2
+
）•（2
-5
）=4
2-5
2-8
•
=4-5-8×
=-5，
由于D是边BC的中点，则
=
（
+
），
|
|2=
2=
（
2+
2+2
•
）=
（7+19-2×5）=4，
即|
|=2．
故选D．
| m |
| n |
| π |
| 3 |
| 1 |
| 2 |
|
| AB |
| m |
| n |
| m |
| n |
| m |
| n |
| 1 |
| 2 |
| AB |
| 7 |
|
| AC |
| m |
| n |
| m |
| n |
| m |
| n |
| 1 |
| 2 |
即有|
| AC |
| 19 |
又
| AB |
| AC |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| 1 |
| 2 |
由于D是边BC的中点，则
| AD |
| 1 |
| 2 |
| AB |
| AC |
|
| AD |
| AD |
| 1 |
| 4 |
| AB |
| AC |
| AB |
| AC |
| 1 |
| 4 |
即|
| AD |
故选D．
点评：本题考查向量的数量积的定义和性质，考查向量的平方即为模的平方，考查运算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
P是椭圆
+
=1（a＞b＞0）上的一个点，F为该椭圆的左焦点，O为坐标原点，且△POF为正三角形．则该椭圆离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、4-2
| ||||
B、2-
| ||||
C、
| ||||
D、
|
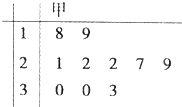某篮球运动员甲参加了10场比赛，他每场比赛得分的茎叶图如图所示，则数据落在区间[22，30）内的概率为（ ）
| A、0.6 | B、0.5 |
| C、0.4 | D、0.3 |
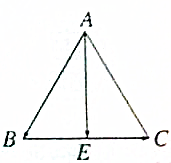如图，已知△ABC是等边三角形．