题目内容
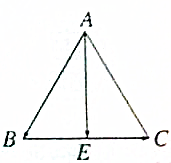如图，已知△ABC是等边三角形．（1）求向量
| AB |
| BC |
（2）若E为BC的中点，求向量
| AE |
| EC |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）由等边三角形的定义和向量夹角的概念，即可得到；
（2）由等边三角形的三线合一，可得AE⊥BC，即可得到所求夹角．
（2）由等边三角形的三线合一，可得AE⊥BC，即可得到所求夹角．
解答：
解：（1）△ABC是等边三角形，则角B=60°，
则向量
与向量
的夹角为180°-60°=120°；
（2）若E为BC的中点，则由等边三角形的性质可得
AE⊥BC，即有向量
与
的夹角为90°．
则向量
| AB |
| BC |
（2）若E为BC的中点，则由等边三角形的性质可得
AE⊥BC，即有向量
| AE |
| EC |
点评：本题考查向量的夹角的大小，注意向量夹角的定义和范围是解题的关键．
练习册系列答案
相关题目
已知单位向量
，
的夹角为
，在△ABC中，
=2
+
，
=2
-5
，D是边BC的中点，则|
|等于（ ）
| m |
| n |
| π |
| 3 |
| AB |
| m |
| n |
| AC |
| m |
| n |
| AD |
| A、12 | ||
B、2
| ||
| C、4 | ||
| D、2 |
从1，2，3，4，5这五个数中，任取两个不同的数，则这两个数之和为3或6的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|