题目内容
若直线y=kx+1（k≠0）与圆x2+（y-1）2=1相交于A，B两点，C点坐标（3，0），若点M（a，b）满足
+
+
=
，则a+b=（ ）
| MA |
| MB |
| MC |
| 0 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点：直线和圆的方程的应用,向量的加法及其几何意义,直线与圆相交的性质
专题：直线与圆
分析：画出图形判断M的特征为三角形的重心，求出M的坐标，即可求出a，b．
解答：
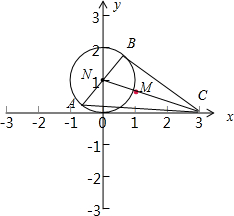解：如图：
直线y=kx+1（k≠0）与圆x2+（y-1）2=1相交于A，B两点，C点坐标（3，0），若点M（a，b）满足
+
+
=
，所以M是三角形ABC的重心，仔细恒过圆的圆心，所以M三等分NC，N（0，1），C（3，0），所以M（1，
），又点M（a，b），即a=1，b=
，
a+b=
．
故选：C．
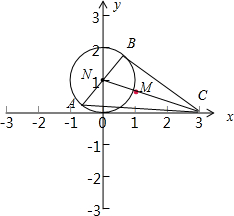解：如图：直线y=kx+1（k≠0）与圆x2+（y-1）2=1相交于A，B两点，C点坐标（3，0），若点M（a，b）满足
| MA |
| MB |
| MC |
| 0 |
| 2 |
| 3 |
| 2 |
| 3 |
a+b=
| 5 |
| 3 |
故选：C．
点评：本题考查仔细与圆的位置关系，的方程的综合应用，向量的应用，考查分析问题解决问题的能力．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
抛物线y2=px（p＞0）的准线方程为x=-
，则p=（ ）
| 1 |
| 4 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知单位向量
，
的夹角为
，在△ABC中，
=2
+
，
=2
-5
，D是边BC的中点，则|
|等于（ ）
| m |
| n |
| π |
| 3 |
| AB |
| m |
| n |
| AC |
| m |
| n |
| AD |
| A、12 | ||
B、2
| ||
| C、4 | ||
| D、2 |
从1，2，3，4，5这五个数中，任取两个不同的数，则这两个数之和为3或6的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|