题目内容
数列{an}满足a1=2，a1+a2+a3=12，且an-2an+1+an+2=0，求数列{an}的前20项和．
考点：数列的求和
专题：等差数列与等比数列
分析：由an-2an+1+an+2=0，推导出数列{an}是等差数列，由此能求出数列{an}的前20项和．
解答：
解：∵an-2an+1+an+2=0，
∴an+an+2=2an+1，
∴数列{an}是等差数列，
∵a1=2，a1+a2+a3=12，
∴3a2=12，解得a2=4，
∴d=a2-a1=4-2=2，
∴数列{an}的前20项和：
S20=20×2+
×2=420．
∴an+an+2=2an+1，
∴数列{an}是等差数列，
∵a1=2，a1+a2+a3=12，
∴3a2=12，解得a2=4，
∴d=a2-a1=4-2=2，
∴数列{an}的前20项和：
S20=20×2+
| 20×19 |
| 2 |
点评：本题考查数列的前20项和的求法，是基础题，解题时要注意等差数列的性质的灵活运用．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
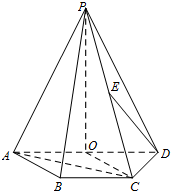如图，四棱锥P-ABCD中，底面ABCD是直角梯形，CD⊥平面PAD，BC∥AD，PA=PD，O，E分别为AD，PC的中点，PO=AD=2BC=2CD．
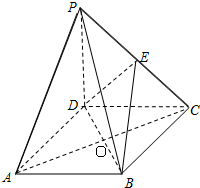如图，在四棱锥P-ABCD中，PD⊥面ABCD，底面ABCD是边长为a的正方形，对角线AC与BD相交于O，且PD=a，E为棱PC的中点．
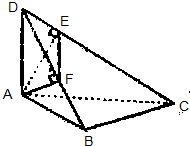如图，在四边形ABCD中，DA⊥平面ABC，∠ABC=90°，AE⊥CD，AF⊥DB，求证：
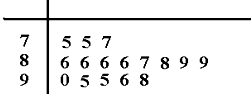某统计部门用“10分制”调查一社区人们对物业管理的“满意度”．现从调查人群中随机抽取16名，以下茎叶图记录了他们的“满意度”分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：